neda.m
کاربر خاکانجمنخورده

- ارسالها
- 1,720
- امتیاز
- 2,683
- نام مرکز سمپاد
- فرزانگان 1
- شهر
- تهران
- دانشگاه
- شهید رجائی تهران
- رشته دانشگاه
- مهندسی عمران - ژئوتکنیک
مسئله پستچی چینی نخستین بار از سوی ریاضیدان چینی به نامMei ko kwan در سال 1960 طرح شد. یک پستچی می خواهد تمامی نامه ها را به مقصد آنها برساند. در حالی که مسافت طی شده کمینه باشد و بعد از پایان کار به نقطه آغاز برگردد. در این کار، باید هر خیابان را حداقل یک بار طی کند و اگر مجبور شود که از مسیری دوبار عبور کند، باید مسیری با کوتاهترین مسافت را انتخاب کند.
راه حل
این مساله را می توان با یک گراف وزن دار فرمول بندی کرد. در این گراف، راس ها متناظر با مقاصد نامه ها و یال ها، متناظر با مسیرهای مواصلاتی بین این مقاصد است و وزن هر یال نیز متناظر با فاصله بین مقاصد است. بنابراین، باید مسیری بسته پیدا کرد که از هر یال دست کم یک بار عبور کرده و در مجموع، کمترین وزن را داشته باشد.
واضح است اگر گراف اویلری باشد، آنگاه هر مسیر اویلری جواب مساله است؛ ولی اگر گراف اویلری نباشد، حل مساله مشکلتر خواهد بود و از حوصله این بحث خارج است. برای حالت خاص، فرض کنید گراف متناظر یک گراف شبه اویلری باشد و دو راس از درجه فرد را با A ، B نشان م دهید. ابتدا، کوتاه ترین مسیر از A به B را بیابید. سپس، با اضافه کردن این مسیر به مسیر شبه اویلری گراف، جواب مساله به دست می آید. برای توصیف بیشتر، گراف شبه اویلری زیر را در نظر بگیرید:
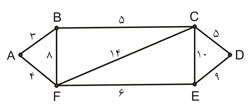
کوتاهترین مسیر از (راس ها از درجه فرد) عبارت است از:
B , A , F , E
و طول این مسیر (مجموع وزن های مسیر) 13= 6+4+3 است.
همچنین، مسیر شبه اویلری عبارت است از:
B , C , D , E , F , A , B , F , C , E
و طول این مسیر شبه اویلری 64 است. پس کوتاه ترین مسیر برای مساله پستچی در گراف فوق عبارت است از:
B , C , D , E , F , A , B , F , C , E , F , A , B
و طول کل آن 77 = 64+13 است.

منبع: دانشنامه ی رشد
راه حل
این مساله را می توان با یک گراف وزن دار فرمول بندی کرد. در این گراف، راس ها متناظر با مقاصد نامه ها و یال ها، متناظر با مسیرهای مواصلاتی بین این مقاصد است و وزن هر یال نیز متناظر با فاصله بین مقاصد است. بنابراین، باید مسیری بسته پیدا کرد که از هر یال دست کم یک بار عبور کرده و در مجموع، کمترین وزن را داشته باشد.
واضح است اگر گراف اویلری باشد، آنگاه هر مسیر اویلری جواب مساله است؛ ولی اگر گراف اویلری نباشد، حل مساله مشکلتر خواهد بود و از حوصله این بحث خارج است. برای حالت خاص، فرض کنید گراف متناظر یک گراف شبه اویلری باشد و دو راس از درجه فرد را با A ، B نشان م دهید. ابتدا، کوتاه ترین مسیر از A به B را بیابید. سپس، با اضافه کردن این مسیر به مسیر شبه اویلری گراف، جواب مساله به دست می آید. برای توصیف بیشتر، گراف شبه اویلری زیر را در نظر بگیرید:

کوتاهترین مسیر از (راس ها از درجه فرد) عبارت است از:
B , A , F , E
و طول این مسیر (مجموع وزن های مسیر) 13= 6+4+3 است.
همچنین، مسیر شبه اویلری عبارت است از:
B , C , D , E , F , A , B , F , C , E
و طول این مسیر شبه اویلری 64 است. پس کوتاه ترین مسیر برای مساله پستچی در گراف فوق عبارت است از:
B , C , D , E , F , A , B , F , C , E , F , A , B
و طول کل آن 77 = 64+13 است.

منبع: دانشنامه ی رشد

