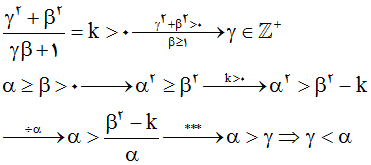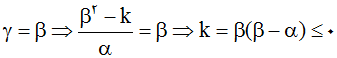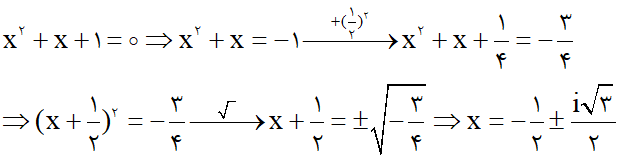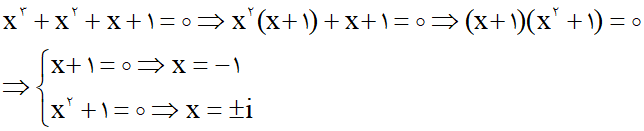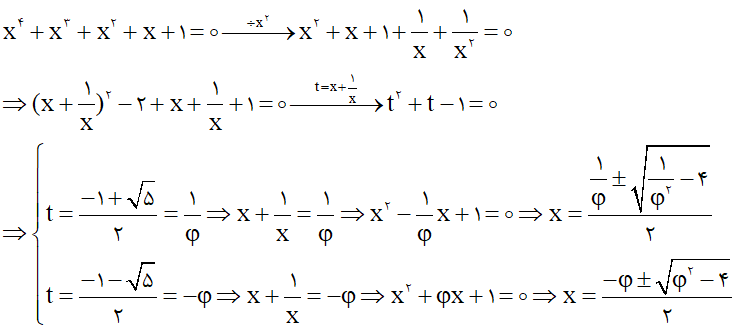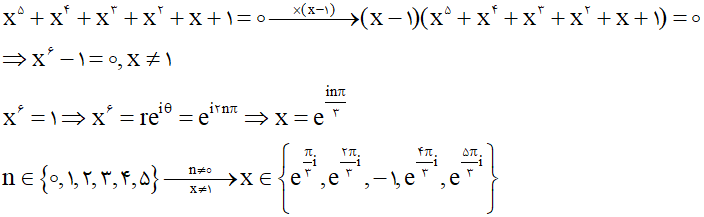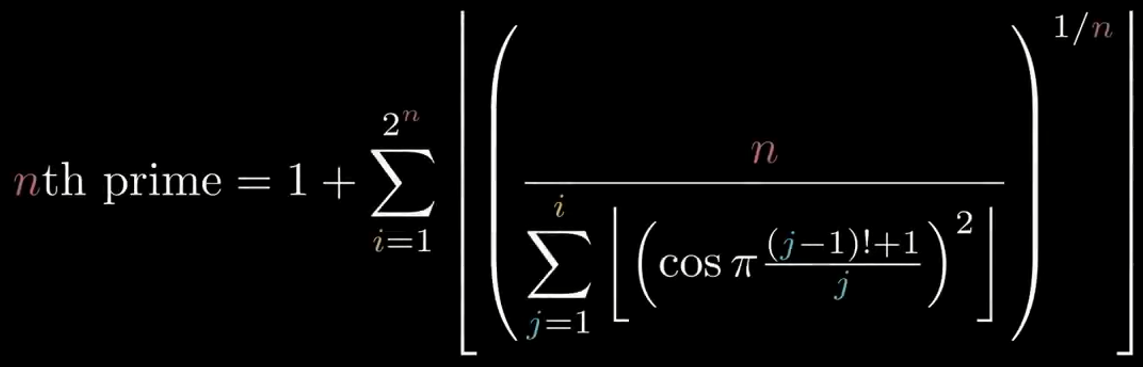قطعاً اینو شنیدید که میگن هیچ فرمولی برای یافتن اعداد اول وجود نداره، خب این تقریباً هم درسته هم غلط!
در سال 1964، فردی به نام C.P. Willans این فرمول غولآسا رو برای یافتن n امین عددِ اول پیدا کرد:
پنیک نکنید، بیاید تا این گندهبک رو به قطعات ریزتری تقسیم و تحلیلش کنیم.
مشخصه که اجزای این فرمول همگی از نکات بیسیک ریاضی و مثلثاتی که باهاشون آشنا هستیم تشکیل شدن؛ فرمول سیگما، تابع جزء صحیح، کسینوس، فاکتوریل و حتی عدد پی. هیچکدوم ربطی به اعداد اول ندارن، اما باور کنید که این ماشین براتون عدد اول تولید میکنه. بهش 1 بدید، بهتون 2 تحویل میده، نخستین عدد اول. بهش 4 بدید، بهتون 7 تحویل میده، چهارمین عدد اول. بهش 1000 بدید، بهتون 7919 تحویل میده، هزارمین عدد اول! فوقالعادهست، نه؟ این چه جمبل و جادوییه؟
قطعاً باید یه ترفندی تو کار باشه چون اعداد اول هیچ قاعدهای ندارن و به طور کاملاً رندوم بین اعداد طبیعی پخش شدن و نباید فرمولی داشته باشن. از طرف دیگه اگه شما این فرمول رو توی زبان برنامهنویسی موردعلاقهتون کدنویسی کنید واقعاً بهتون عدد اول میده منتها در مقادیر کمِ n این کار رو سریع انجام میده و در مقادیر بیشتر سرعتش کند میشه و این خودش نشانی از کاریه که در عمل این فرمول داره انجام میده.
خب بیایم بررسی کنیم که داره چه غلطی میکنه.
اول بریم سراغ درونیترین لایه، یعنی
(جِی منهای 1)فاکتوریل. چیز خاصی نیست، عدد طبیعی میدی، یکی کم میکنه و بعد متوالیاً در اعداد طبیعی ماقبلش تا برسه به 1 ضرب میکنه که همون مفهوم فاکتوریله. ویلنز گفته به این مقدار یکی اضافه کنین و حاصل رو تقسیم بر جی کنین. به عنوان مثال اگه جی رو 5 درنظر بگیریم، 4فاکتوریل میشه 24، یکی اضافه کنیم میشه 25، حاصل رو بر 5 تقسیم کنیم میشه 5. اگه جی رو 6 درنظر بگیریم، 5فاکتوریل میشه 120، یکی اضافه کنیم میشه 121، و حاصل تقسیم بر 6 یه عدد کسری میشه. بیایم و یه جدول مقادیر واسه چن ورودی مختلف از 1 تا 11 براش بنویسیم:
متوجه الگوی خاصی شدید؟ وقتی جی عدد اول (بجز یک) باشه، حاصل همیشه عدد صحیحه، و در غیر این صورت عددی ناصحیح. و این همون راز درون فرمول ویلنزه. الگوریتمی که اعداد اول رو برامون پیدا میکنه. این در واقع چیزی نیست جز همون
قضیهٔ ویلسون، که در ریاضیات گسستهٔ دبیرستان باهاش آشنا شدیم و میگه اگر p (یا در اینجا همون j خودمون) عددی اول باشه، !(p-1) به پیمانهٔ p همیشه منفی یک میشه. یا به عبارت دیگه،
جی منهای یک فاکتوریل رو اگه علاوۀ یک کنیم، اگر جی عددی اول یا خودِ 1 باشه همواره بر جی بخشپذیره. این یعنی ما یک
prime number detector ساختیم! حالا چطور میتونیم یک «شناساگر اعداد اول» رو تبدیلش کنیم به یک «مولّد اعداد اول»؟
راه کمترخلاقانهای که براش وجود داره اینه که مثلاً اگر بخوایم 4 امین عدد اول رو پیدا کنیم، باید بگردیم ببینیم توی این سری، چهارمین عدد صحیحی که بعد از 1 تولید میشه چیه و همونجا توقف کنیم و بگیم آها پیداش کردیم. کاری که ویلنز انجام داده اینه که این راه غیرهوشمندانه رو هوشمندانهش کرده. چون خب برنامهنویسا میتونستن همین فرمول رو هم استفاده کنن و یه لوپ تشکیل بدن و بگردن دونه دونه چک کنن. ولی اگه ما زبان برنامهنویسی در اختیارمون نباشه چی؟ ویلنز با کمک ریاضیاتِ دم دستی تونست این کارو بکنه.
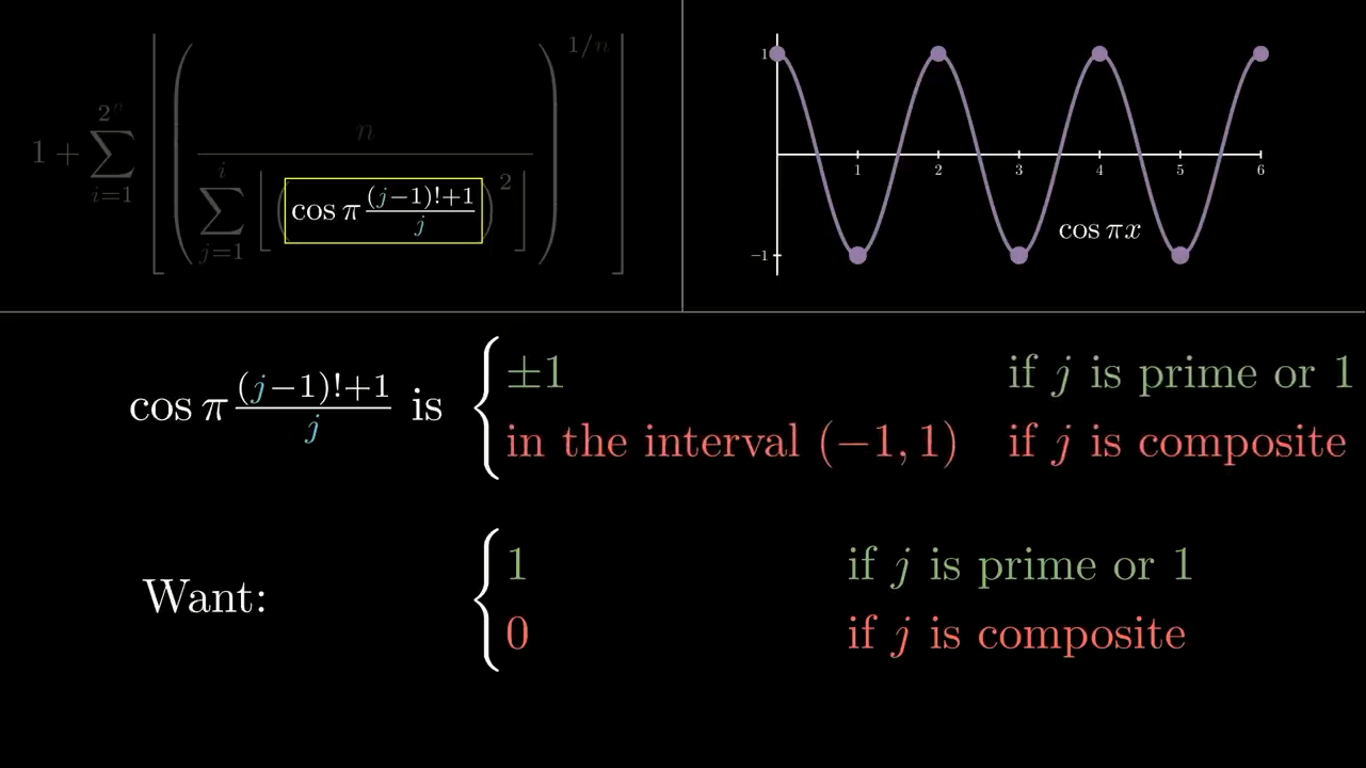
اول لازمه prime detector مون رو کمی تغییر بدیم. اگر به شکل زیر درش بیاریم بهتر میشه و کار باهاش آسونتره:
واسه اینکه بخوایم اعداد صحیح رو به 1 و اعداد ناصحیح رو به 0 تبدیل کنیم، باید integer detector وارد عمل کنیم. حالا چه جور تابعی میتونه چنین کاری برامون انجام بده؟ اگه برگردیم به فرمول ویلنز، میبینیم که چه اتفاقی بعدش میافته. قدم بعدی، اینه حاصلِ اون کسر ویلسون رو در پی ضرب کرده و ازش کسینوس گرفته. نمودار تابع کسینوس پیایکس رو اگر رسم کنیم، میبینیم که به ازای مقادیر صحیح ایکس، به اکسترمم خودش یعنی 1 و 1- میرسه و در سایر موارد مقداری بین این دو عدد هستش. بیایم و تابع رو بازنویسی کنیم:
واسه اینکه از شر منفی خلاص شیم، اومده تابع رو به توان 2 رسونده. اینطوری هم 1- همیشه به 1+ تبدیل شده، هم اینکه مقادیر بین 1- تا 1+ به مقادیر بین 0 تا 1 تبدیل شده و حالا اگر ازش جز صحیح بگیریم، میرسیم به همون چیزی که میخوایم!
حالا کافیه که تعداد این 1 ها رو بشماریم.
اگر از جی مساوی 1 تا هر مقداری که مدنظرمونه سیگما بگیریم، حاصل، میشه تعداد اعداد اولی که در اون بازه وجود داره، به اضافۀ 1 (چون داره خود 1 رو هم برامون میشمره). به عنوان مثال از جی مساوی 1 تا 10 رو ببینید چه اتفاقی میافته:
ولی خب ما که نیومدیم فقط تعداد اعداد اول در یک بازه رو پیدا کنیم، اومدیم nامین عدد اولو پیدا کنیم. میدونیم از 1 تا 10، چهارتا عدد اول وجود داره، ولی چهارمین عدد اول چیه؟ خب این
تابع معکوس چیزیه که ما اینجا داریم. ایدهش اینه که یعنی اگه ما دنبال چهارمین عدد اول میگردیم، باید پیوسته بپرسیم آیا تعداد اعداد اول قبل از فلان عدد، کمتر از 4عه یا نه؟ تعداد اعداد اول قبل از 1 از 4 کمتره، قبل از 2 از 4 کمتره، قبل از 3 از 4 کمتره، قبل از 4 از 4 کمتره و ... تا میرسیم به جایی که جواب خیر میشه و درست همونجایی خیر میشه که به چهارمین عدد اول رسیده باشیم. پس سایر فرمول ویلنز داره همین کار رو میکنه، که
آیا تعداد اعداد اول ماقبل آی، از n کمتر است؟ (به ازای i متغیر) . و خب این زمانی به خیر تبدیل میشه که ما به n امین عدد اولمون رسیده باشیم. پیچیده که نیست، نه؟
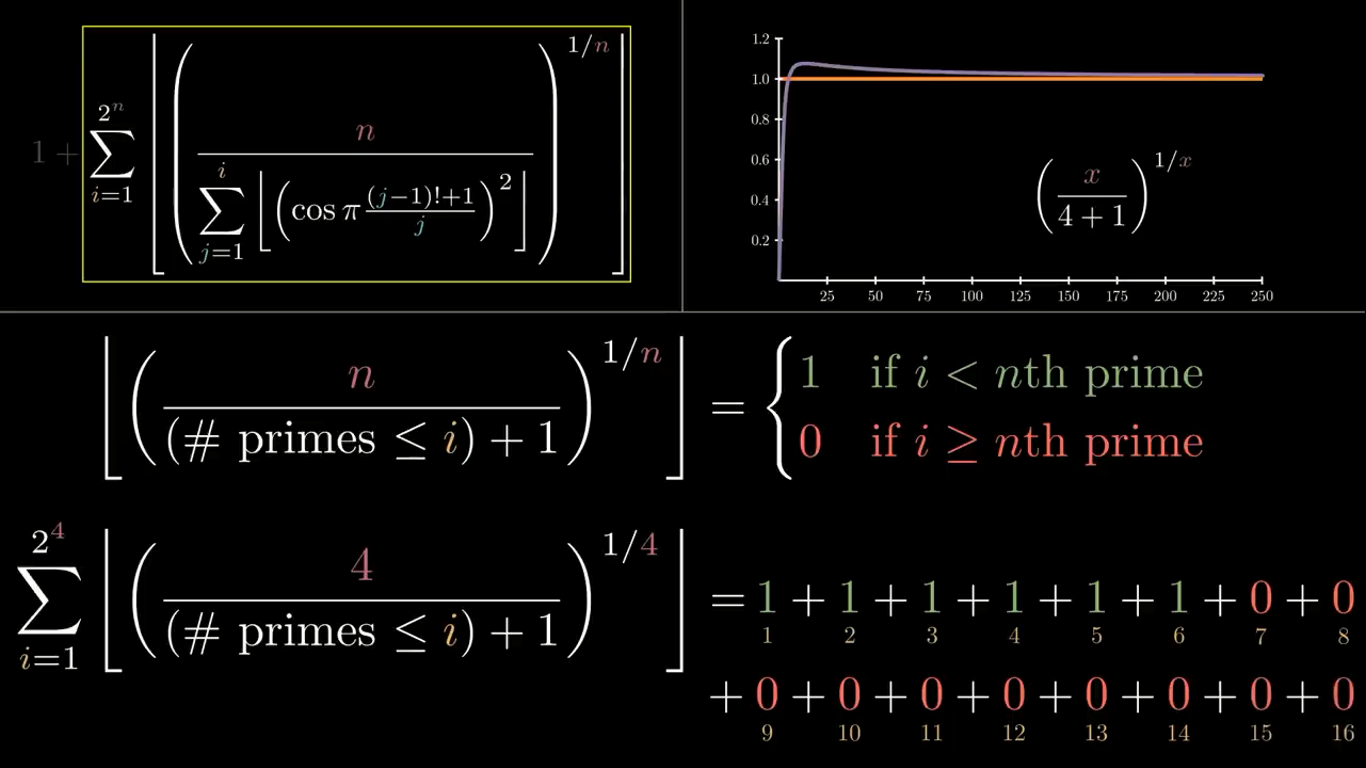
بقیۀ کار نیاز به کمی مهندسی داره. در قسمت بعدی فرمول ویلنز، میایم و حاصل n تقسیم بر اون ماشین یابندۀ تعداد اعداد اول رو بدست میاریم و بعد کل چیزی که حاصل شده رو به توان یک تقسیم بر n میرسونیم. در اینجا n مقدار ثابت ماست، ولی فهمش برامون سادهتر میشه اگر i رو ثابت نگه داریم و n رو تغییر بدیم. آی رو همون 10 فرض بگیرید. میدونیم که 4 تا عدد اول قبلش وجود داره، پس ماشین برامون 5 تولید میکنه. نمودار تابع «ایکس پنجم به توان یک ایکسم» رو رسم میکنیم و بعد ازش جز صحیح میگیریم. نقطۀ پیکش پس از جز صحیح گرفتن، 1 عه. ببینیم کجا به 1 میرسه. درست وقتی که ایکس به 5 میرسه. منطقی هم هست چون اگه 5 بذاریم حاصل میشه 1 به توان یک پنجم که همون 1 عه. به ازای مقادیر بعد از 5 هم ظاهرا نمودار داره بالاتر میره ولی اینطور نیست و وقتی به ماکزیمم خودش رسید میاد پایین. معنیش اینه اگه جز صحیح بگیریم،
به ازای اعداد طبیعی بیشتر از 4، 1 به دست میاریم و به ازای اعداد طبیعی کمتر مساوی 4، 0 به دست میاریم.
میشه تعمیمش هم داد. و خب این «4» ای که قرار دادیم، همون تعداد اعداد اول قبل از 10 عه و میتونیم به جای 10، متغیر i رو بگذاریم، و سپس به تابع دوضابطهای زیر برسیم:
دقیقاً داره به پرسشی که ما مطرحش کردیم به عنوان تابع معکوس، جواب میده:
آیا تعداد اعداد اول قبل از آی، کمتر از n عه؟ تو فرمول ویلنز هم n ثابت بود و i تغییر میکرد. این سوال، درست عین اینه که بپرسیم
آیا n امین عدد اول، بزرگتر از i عه؟ مثال بزنیم تا برامون واضحتر بشه:
آی رو همون 10 در نظر بگیریم، ماشین پایین بهمون 5 تحویل میده. توی ضابطۀ نماییِ نهایی، وقتی جز صحیح بگیریم، اگر n پنج یا بیشتر باشه 1 به دست میاریم (تعداد اعداد اول قبل از 10، چار تاست) و اگر n برابر 4 یا کمتر باشه، خروجیمون 0 عه. حالا معادلسازی کنیم؛ پنجمین عدد اول، قطعاً از 10 بیشتره! یا میشه گفت n امین عدد اول قطعاً از i بزرگتره. حالا بیایم بازنویسی کنیم و روی i تمرکز کنیم چون قراره i تغییر کنه نه n.
این
یک ماشینِ یابندۀ تموم i هاییه که از n امین عدد اول کمتر هستن. حالا در قدم نهایی، میایم و تمام این i ها رو از 1 تا 2 به توان n جمع میزنیم. مثال:
اگر n = 4 باشه، میذاریم i از 1 تا 16 تغییر کنه. برای هر آی که از چهارمین عدد اولمون کمتر باشن، یه 1 تحویل میگیریم. زمانی که به 7 برسیم، دیگه 0 تحویل میگیریم. جمعشون میشه 6، که یکی کمتر از 7 یا همون چهارمین عدد اول ماست.
حالا سوالی که پیش میاد اینه که چرا تا 16 باید پیش بریم؟ این 2 به توان n صرفاً نوعی
گارانتیه تا خیالمون راحت باشه دیگه 1 به دست نمیاریم و منبعد 0 تحویل میگیریم. چون نمیدونیم n امین عدد اول چقدره و تا کجا باید پیش بریم. در نظریۀ اعداد،
اصل برتراند میگه برای هر عدد طبیعی بزرگتر مساوی 2، عدد اولی مانند p هست به طوری که p بین n و 2n واقع شده. یعنی عدد اولی بین 2 و 4 هست (3)، عدد اولی بین 4 و 8 هست (5)، عدد اولی بین 8 و 16 هست (11) و ... . چون 2 خودش اوله،
اصل برتراند تضمین میکنه n تا عدد اول بین 1 تا 2 به نمای n موجوده. پس n امین عدد اول قطعاً از 2 به نمای n کمتره. در واقعیت هم n امین عدد اول خیلی کوچیکتر از 2 به نمای n عه، ولی خب ویلنز براش این گپِ بزرگ که محاسبه رو طولانی میکرد اهمیت نداشت.
در نهایت هم مشخصه که چرا
به علاوۀ یک میکنیم.
خب بچهها! ما یک فرمول برای به دست اوردن n امین عدد اول پیدا کردیم! ولی ریدیم، چرا؟ چون این فرمول به هیچ عنوان کارامد نیست و خیلی محاسبات سنگینی احتیاجه، عین بروت فورس میمونه.