erfan_ashorian
کاربر حرفهای

- ارسالها
- 397
- امتیاز
- 1,241
- نام مرکز سمپاد
- 2
- شهر
- تهران
- دانشگاه
- _ان شا الله قوزاباد
- رشته دانشگاه
- _علوم کامپیوتر(البته در این
سلام به همه خیلی وقت بود میخواستم این پستو بزارم حسش نمیشود دیدم جمعستو حس درس خوندن نیست گفتم یه کار مفید بکنم!
خب به ترتیب شروع میکنیم به توضیح:
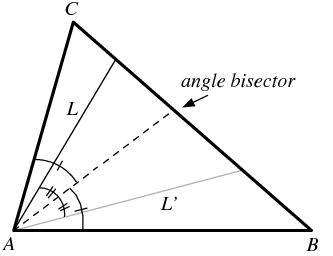
در شکل بالا ایزوگونال!خط Lنسبت به زاویه ی CABخط Lپریم میباشد زیرا این دو خط نسبت به نیمساز زاویه ی CABقرینه اند
خب حالا که تعریف رو فهمیدید چند تا تمرین اسون!
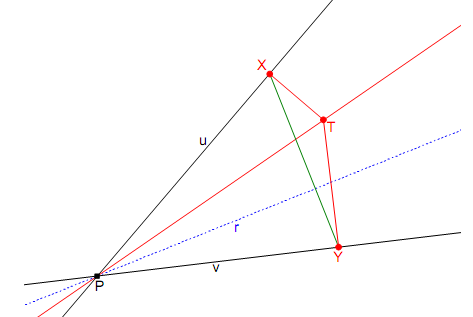
1)فرض کنید دو تا خط UوVهمدیگر را در P قطع کرده باشند فرض کنید تصویر نقطه ی دلخواه Tروی دو خط U,Vبه ترتیب X,Yباشد ثابت کنید ایزوگونال خط PTنسبت به دو خط U,Vبر خط XYعمود است !
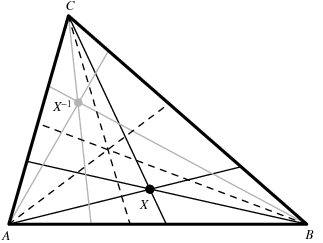
حالا فرض کنید که یک که یک نقطه در مثلث ABC داریم به اسم X حالا قضیه ی زیر را داریم:
قضیه 1:اگر ایزوگونال خطوط XAوXBوXCرا نسبت به زوایای CABوABCوACBرسم کنیم خطوط حاصل همدیگر را در نقطه ای مثل X_1قطع میکنند.
اثبات راهنمایی)از قضیه ی سینوسی سوا استفاده کنید.
راهنمایی)از قضیه ی سینوسی سوا استفاده کنید.
به نقطه ی X-1isogonal conjugate
نقطه ی Xنسبت به مثلث ABCمیگویند.
تمرین:
1)ثابت کنید isogonal conjugate مرکز دایره محیطی مرکز ارتفاعی مثلث است.
2)ثابت کنید isogonal conjugate مرکز دایره محاطی خودش میباشد.
تعریف :Symmedian Point
isogonal conjugateمرکز ثقل مثلث را Symmedian Pointمینامیم که ان را با حرف kنشان میدهند!
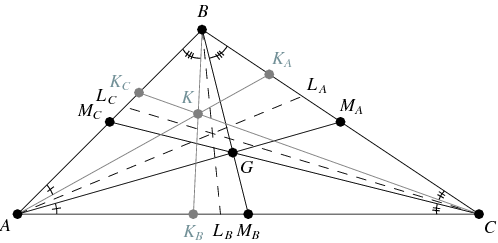
تعریف:مثلث پدال
فرض کنید نقطه ای دلخواه در صفحه داشته باشیم رئوس مثلث پدال این نقطه نسبت به مثلث ABCعبارت اند از عمود های وارد از این نقطه بر اضلاع مثلث.
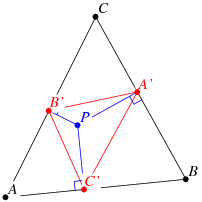
قضیه مهم و جالب:ثابت کنید مرکز ثقل هر مثلث پدالی در صفحه symmedian point یا همان kمیباشد!
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=47&t=441141
این مقاله ادامه دارد.............
منابع:
artofproblemsolving.com
http://www.cut-the-knot.org/geometry.shtml
http://www.cip.ifi.lmu.de/~grinberg/
خب به ترتیب شروع میکنیم به توضیح:

در شکل بالا ایزوگونال!خط Lنسبت به زاویه ی CABخط Lپریم میباشد زیرا این دو خط نسبت به نیمساز زاویه ی CABقرینه اند
خب حالا که تعریف رو فهمیدید چند تا تمرین اسون!
1)فرض کنید دو تا خط UوVهمدیگر را در P قطع کرده باشند فرض کنید تصویر نقطه ی دلخواه Tروی دو خط U,Vبه ترتیب X,Yباشد ثابت کنید ایزوگونال خط PTنسبت به دو خط U,Vبر خط XYعمود است !

حالا فرض کنید که یک که یک نقطه در مثلث ABC داریم به اسم X حالا قضیه ی زیر را داریم:
قضیه 1:اگر ایزوگونال خطوط XAوXBوXCرا نسبت به زوایای CABوABCوACBرسم کنیم خطوط حاصل همدیگر را در نقطه ای مثل X_1قطع میکنند.

اثبات
 راهنمایی)از قضیه ی سینوسی سوا استفاده کنید.
راهنمایی)از قضیه ی سینوسی سوا استفاده کنید.به نقطه ی X-1isogonal conjugate
نقطه ی Xنسبت به مثلث ABCمیگویند.
تمرین:
1)ثابت کنید isogonal conjugate مرکز دایره محیطی مرکز ارتفاعی مثلث است.
2)ثابت کنید isogonal conjugate مرکز دایره محاطی خودش میباشد.
تعریف :Symmedian Point
isogonal conjugateمرکز ثقل مثلث را Symmedian Pointمینامیم که ان را با حرف kنشان میدهند!

تعریف:مثلث پدال
فرض کنید نقطه ای دلخواه در صفحه داشته باشیم رئوس مثلث پدال این نقطه نسبت به مثلث ABCعبارت اند از عمود های وارد از این نقطه بر اضلاع مثلث.

قضیه مهم و جالب:ثابت کنید مرکز ثقل هر مثلث پدالی در صفحه symmedian point یا همان kمیباشد!
http://www.artofproblemsolving.com/Forum/viewtopic.php?f=47&t=441141
این مقاله ادامه دارد.............
منابع:
artofproblemsolving.com
http://www.cut-the-knot.org/geometry.shtml
http://www.cip.ifi.lmu.de/~grinberg/


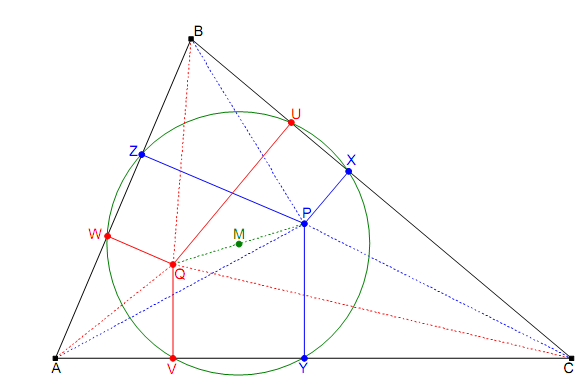
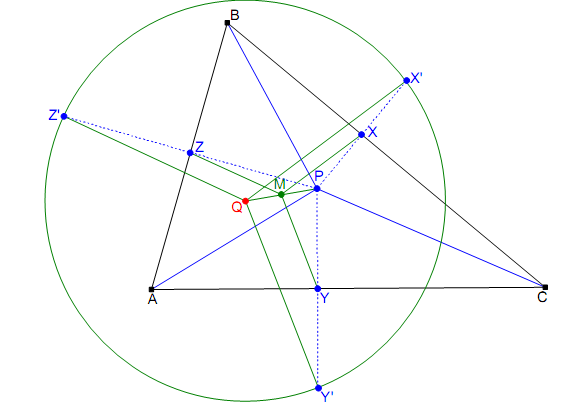



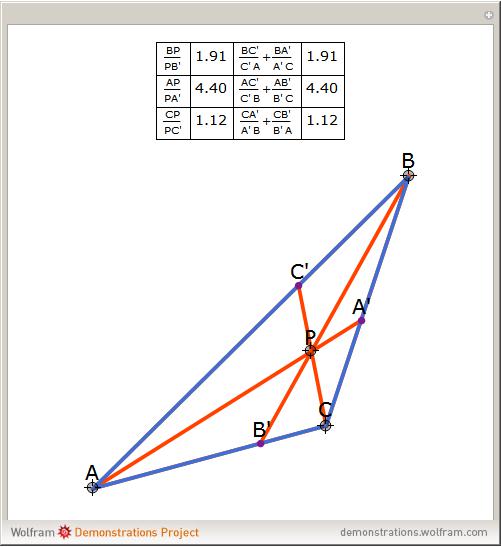

 یعنی یحتمل ممنوعه دیگه نیس؟!)خو پس چه مرضیه من اینو میگم؟به این درد میخوره که تا میخواین یه مساله رو چک کنین درسته یا نه یا مثلا چند تا نقطه رویه خط هستن یا نه یا از این جور کارا به درد میخوره. ..
یعنی یحتمل ممنوعه دیگه نیس؟!)خو پس چه مرضیه من اینو میگم؟به این درد میخوره که تا میخواین یه مساله رو چک کنین درسته یا نه یا مثلا چند تا نقطه رویه خط هستن یا نه یا از این جور کارا به درد میخوره. .. 