- ارسالها
- 1,667
- امتیاز
- 6,103
- نام مرکز سمپاد
- شهید بهشتی
- شهر
- شهرکرد
- سال فارغ التحصیلی
- 92
- دانشگاه
- صنعتی شریف
- رشته دانشگاه
- مهندسی کامپیوتر- نرم افزار
پاسخ : استقرا
ابتدا فرض کینم n=1 باشه حکم تبدیل به این میشه :
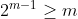
این حکمو 2باره با استقرا ثابت میکنیم که اثباتش خیلی آسونه نیازی به نوشتن نیست .
الان پایه استقرا اثبات شد .
فرض کینم حکم به ازای n=k برقرار باشه داریم :

درنتیجه داریم


از این 2تا حکمو نتیجه میگیریم یعنی

B-)
روی n استقرا میزنیمبه نقل از ๖ۣۜNima :اگر m و n عدد هایی طبیعی باشند ثابت کنید:
2 به توان m+n-2 بزرگتر مساوی m * n است.
B-)
ابتدا فرض کینم n=1 باشه حکم تبدیل به این میشه :
این حکمو 2باره با استقرا ثابت میکنیم که اثباتش خیلی آسونه نیازی به نوشتن نیست .
الان پایه استقرا اثبات شد .
فرض کینم حکم به ازای n=k برقرار باشه داریم :
درنتیجه داریم
از این 2تا حکمو نتیجه میگیریم یعنی
B-)











