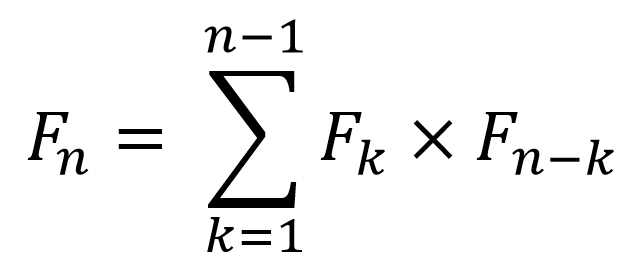senatoor
کاربر فعال

- ارسالها
- 51
- امتیاز
- 205
پاسخ : سوالات ترکیبیات
خب حالا ما تعداد مستطیل های دو در سه رو میشماریم ضرب در چهار میکنیم
تعداد مستطیل های سه در دو هم که کاری نداره شمردنش میشه 6*7*2 حالا حاصل اینو که میشه 84 رو ضرب در چهار میکنیم تمام
حالا جواب رو ببین درسته شاید سوتی هم داده باشم وسطش
قبول داری دوتا اسب فقط میتونن به صورت L هم دیگه رو تهدید کنن؟حالا شکل L چیه؟ببین تو هر مستطیل دو در سه انتخاب کنی دقیقا 4 تا حالت داره برا تهدید اینم که درکش اسونه؟به نقل از TheBest444 :یه سوال آسون شمارشی(لطفا توضیح هم بدین) :
به چند طریق میتوان یک مهره اسب سفید و یک مهره اسب سیاه را در یک جدول 8x8 (هشت در هشت) قرار داد به طوری که یکدیگر را تهدید کنند؟
خب حالا ما تعداد مستطیل های دو در سه رو میشماریم ضرب در چهار میکنیم
تعداد مستطیل های سه در دو هم که کاری نداره شمردنش میشه 6*7*2 حالا حاصل اینو که میشه 84 رو ضرب در چهار میکنیم تمام
حالا جواب رو ببین درسته شاید سوتی هم داده باشم وسطش