با توجه به لگاریتم چند جوابه ای که اویلر تعریف میکنه عدد نپر به توان اعداد مختلط یه تابع یک به یک نیست که بتونیم از برابر شدن نپر به توان یک ایکس مختلط با نپر به توان یک وای مختلط نتیجه بگیریم که ایکس و وای برابرند. درواقع اینجا لگاریتم هاشون برابرند ولی خودشون نیستند.که البته الان نمیدونم درگیر اعداد مختلطش شدم یا نه.به نقل از کیارش :تشکّر میکنم بابت ایدهی خوب مدیر!
خودتونو درگیر اعداد مختلط و اینهاش نکنید. مشکلش سادهتر از این حرفاست.
درسته. البته اینجا خودشون برابرند ولی لگاریتمهاشون برابر نیستن.به نقل از Dorna :
الان این چیزی که من گفتم صفرو با صفر ساده نمیکرد دیگه!به نقل از K.A :
مشکلش اینجاست که اصلا این دو تا منحنی همدیگرو قطع نمیکنن، اگه معادله منحنی ها رو مساوی هم قرار بدیم معادله ی درجه دومی به دست میاد که ریشه نداره! (دلتاش منفیه) پس کلا این وتر مشترک به دست اومده یه چیز موهومیه.به نقل از Dorna :خب گویا مدیر تایید کرد و الان من برای ادامه تاپیک باید پست بگذارم...
دو تا منحنیورو داریم. اگه این دو معادله رو با هم جمع کنیم یه خط داریم. از اونجایی که از هر دو نقطه فقط و فقط یه خط میگذره و این خط از اشتراک دو رابطه به دست اومده و نقاط برخورد دو منحنی روی این خط قرار داره پس این خط همون وتر مشترک دو منحنیه:
یه دستگاه مختصات جدید با دوران دستگاه مختصات با زاویه آرک سینوس شش دهم تعریف میکنیم و معادله ی منحنی اول رو توی دستگاه مختصات جدید به دست میاریم:
و معادله ی وتر مشترک رو هم تو دستگاه مختصات جدید به دست میاریم:
حالا با جایگزین کردن ایکس طبق x=7y-5 در منحی نقاط برخورد وتر مشترک و منحنی رو توی دستگاه مختصات جدید به دست میاریم:
و این معادله در اعداد حقیقی جوابی نداره. یعنی وتر مشترک با منحنی در دستگاه مختصات جدید برخورد نمیکنه.
WOW... شما هم به همون چيزي فك كردي كه من فك مي كردم؟!!!!!!!!!!!!!!!!!!!به نقل از R@na96 :
فقط فرقمون اينه كه من بعد از اين كه فهميدم گفتم شايد مشكل از من بوده!!! اون وخ نشستم عين احمقا كلا دو تا منحني رو كشيدم كه عملا ببينم!!!!!! 
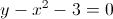
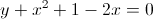
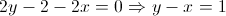
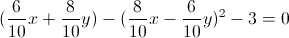
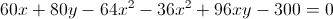
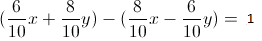
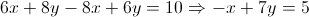
(كلا داراي همچين اعتماد بنفس سرشاريم )
#