Fliqpy
کاربر نیمهحرفهای

- ارسالها
- 181
- امتیاز
- 303
- نام مرکز سمپاد
- غیر انتفاعی علامه حلی 3
- شهر
- تهران
- مدال المپیاد
- هر جوری حساب میکنم افتخار نمیکنم بهش
- دانشگاه
- شريف
- رشته دانشگاه
- نرم افزار
سلام
جالبه بدونيد كه المپياد هندسه هم مثل المپياد جهاني شورت ليست داشته.
سوالات شورت ليست المپياد هندسه ٩٣ رو اينجا قرار ميدم.
سوال ١)
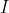 مركز دايره محاطي مثلث
مركز دايره محاطي مثلث
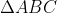 است و
است و
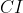 و
و
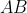 در
در
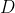 متقاطعند. وسط كمان
متقاطعند. وسط كمان
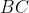 از دايره محيطي كه شامل
از دايره محيطي كه شامل
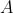 هست را
هست را
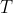 ميناميم. فرض كنيد محل برخورد
ميناميم. فرض كنيد محل برخورد
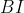 و دايره محيطي
و دايره محيطي
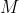 باشد. ثابت كنيد اگر محل برخورد
باشد. ثابت كنيد اگر محل برخورد
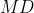 و
و
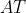 برابر
برابر
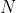 باشد آنگاه
باشد آنگاه
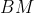 و
و
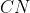 موازيند.
موازيند.
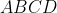 و
و
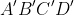 دو متوازي الاضلاع باشند به طوري كه
دو متوازي الاضلاع باشند به طوري كه
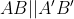 و
و
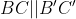 و
و
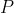 محل برخورد
محل برخورد
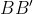 و
و
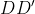 باشد، آنگاه همخطي
باشد، آنگاه همخطي
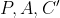 با همخطي
با همخطي
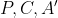 معادل است.
معادل است.
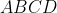 يك چهارضلعي محاطي باشد كه در آن
يك چهارضلعي محاطي باشد كه در آن
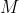 وسط كمان
وسط كمان
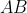 و
و
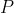 محل برخورد قطرهاي چهارضلعي است. ثابت كنيد اگر
محل برخورد قطرهاي چهارضلعي است. ثابت كنيد اگر
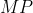 بر
بر
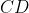 عمود باشد و
عمود باشد و
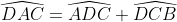 آنگاه چهارضلعي ما يك ذوزنقه است.
آنگاه چهارضلعي ما يك ذوزنقه است.
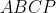 يك چهاروجهي باشد و
يك چهاروجهي باشد و
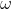 كره اي باشد كه دواير محاطي مثلثهاي
كره اي باشد كه دواير محاطي مثلثهاي
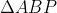 و
و
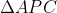 و
و
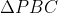 روي آن قرار دارند. ثابت كنيد دايره محاطي مثلث
روي آن قرار دارند. ثابت كنيد دايره محاطي مثلث
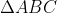 نيز روي كره
نيز روي كره
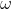 قرار دارد.
قرار دارد.
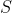 ،
،
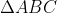 محل برخورد
محل برخورد
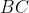 و مماس مرسوم از
و مماس مرسوم از
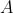 بر دايره محيطي است. فرض كنيد
بر دايره محيطي است. فرض كنيد
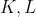 نقاطي روي
نقاطي روي
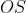 باشند به طوري كه
باشند به طوري كه
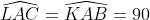 .
.
ثابت كنيد
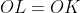 .
.
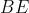 و
و
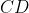 ارتفاع هاي مثلث
ارتفاع هاي مثلث
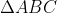 باشند كه در
باشند كه در
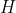 متقاطعند. قرينه
متقاطعند. قرينه
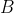 و
و
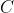 نسبت به
نسبت به
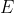 و
و
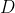 به ترتيب
به ترتيب
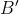 و
و
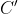 هستند. فرض كنيد مركز دايره محيطي
هستند. فرض كنيد مركز دايره محيطي
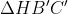 برابر
برابر
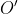 باشد. همچنين وسط
باشد. همچنين وسط
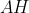 را
را
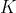 در نظر بگيريد.
در نظر بگيريد.
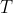 محل برخورد
محل برخورد
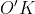 و
و
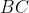 است. ثابت كنيد
است. ثابت كنيد
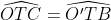 كه در آن
كه در آن
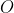 مركز دايره محيطي مثلث است.
مركز دايره محيطي مثلث است.
جالبه بدونيد كه المپياد هندسه هم مثل المپياد جهاني شورت ليست داشته.
سوالات شورت ليست المپياد هندسه ٩٣ رو اينجا قرار ميدم.
سوال ١)
(طرح علي ذوعلم)
سوال ٢) اگر (طرح علي ذوعلم)
٣) فرض كنيد (طرح مرتضي ثقفيان)
٤)فرض كنيد (طرح مرتضي ثقفيان)
٥) در مثلث ثابت كنيد
(طرح علي زماني)
٦)فرض كنيد (طرح علي زماني)




