Fliqpy
کاربر نیمهحرفهای
- ارسالها
- 181
- امتیاز
- 303
- نام مرکز سمپاد
- غیر انتفاعی علامه حلی 3
- شهر
- تهران
- مدال المپیاد
- هر جوری حساب میکنم افتخار نمیکنم بهش
- دانشگاه
- شريف
- رشته دانشگاه
- نرم افزار
پاسخ : سوالات نظریه اعداد هم سطح مرحله دوّم
7) فرض کنید P مجموعه تمام اعداد اول باشد.هم چنین فرض کنید M زیر مجموعه ای از آن باشد به طوری که به ازای هر زیر مجموعه ناتهی و متناهی از M مانند t تمام عوامل اول
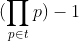
عضو M باشند. ثابت کنید P=M
7) فرض کنید P مجموعه تمام اعداد اول باشد.هم چنین فرض کنید M زیر مجموعه ای از آن باشد به طوری که به ازای هر زیر مجموعه ناتهی و متناهی از M مانند t تمام عوامل اول
عضو M باشند. ثابت کنید P=M
- ارسالها
- 94
- امتیاز
- 355
- نام مرکز سمپاد
- فرزانگان حضرت زینب (س) ری
- شهر
- تهران
- سال فارغ التحصیلی
- 95
- مدال المپیاد
- فقط مرحله 1 ریاضی...المپیاد هندسه شریف
- دانشگاه
- علم و صنعت
- رشته دانشگاه
- مهندسی ماشین های ریلی:)
پاسخ : سوالات نظریه اعداد هم سطح مرحله دوّم
سوال 9)تمام n هایی را بیابید که در شرط زیر صدق کند:
سوال 9)تمام n هایی را بیابید که در شرط زیر صدق کند:
ehsan-mokhtarian
کاربر فوقفعال
- ارسالها
- 104
- امتیاز
- 361
- نام مرکز سمپاد
- علامه حلی 1
- شهر
- تهران
- مدال المپیاد
- نقره ریاضی 1391 طلا ریاضی 1392
پاسخ : سوالات نظریه اعداد هم سطح مرحله دوّم
پاسخ : سوالات نظریه اعداد هم سطح مرحله دوّم
به غیر حالت های خاص توان 2 در
)
بیشتر از توان 2 توی n می شه. حالت های خاصی که باید این جا بررسی کنیم اینا هستن:
1)
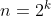
2)
=2^{k})
3)
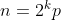که
)
بررسی حالت های 1 و 2 راحته و فک کنم به 3وn=2 برسه. حالت 3 رو هم با توجه به این که
\leq&space;n)
بدیهی می شه ...
اول راحت اثبات می شه که تعداد اعضای M نا متناهی هست. با برهان خلف فرض کنید که p در m نیست. حالا t را شامل p-1 عدد در نظر می گیریم که به پیمانه ی p یکسان هستند . حالا طبق فرما p اون عبارت رو عاد می کنه پس p در M هست که تناقضه ...به نقل از The Overlord :7) فرض کنید P مجموعه تمام اعداد اول باشد.هم چنین فرض کنید M زیر مجموعه ای از آن باشد به طوری که به ازای هر زیر مجموعه ناتهی و متناهی از M مانند t تمام عوامل اول
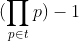
عضو M باشند. ثابت کنید P=M
پاسخ : سوالات نظریه اعداد هم سطح مرحله دوّم
به نقل از N_MATHS :سوال 9)تمام n هایی را بیابید که در شرط زیر صدق کند
به غیر حالت های خاص توان 2 در
1)
2)
3)
بررسی حالت های 1 و 2 راحته و فک کنم به 3وn=2 برسه. حالت 3 رو هم با توجه به این که
Phanntom
کاربر فوقفعال
- ارسالها
- 115
- امتیاز
- 364
- نام مرکز سمپاد
- helli
- شهر
- تهران
- مدال المپیاد
- سابقه دارم!
- دانشگاه
- light massage(پیام نور)
پاسخ : سوالات نظریه اعداد هم سطح مرحله دوّم
اعداد طبیعی a,b چنان هستند که اعداد 15a+16b و 16a+15b هر دو مربع کامل هستند. کمترین مقداری که مینیمم این دو مربع کامل میتواند بگیری چند است؟
ویرایش : بله بله درسته حرف شما
اعداد طبیعی a,b چنان هستند که اعداد 15a+16b و 16a+15b هر دو مربع کامل هستند. کمترین مقداری که مینیمم این دو مربع کامل میتواند بگیری چند است؟
ویرایش : بله بله درسته حرف شما
fitmal
کاربر فوقحرفهای
- ارسالها
- 812
- امتیاز
- 3,334
- نام مرکز سمپاد
- farzanegan 2
- شهر
- کرمان (1 ر) - تهران (بقیه)
- مدال المپیاد
- یه سری مرحله 1 :-" 1 مرحله 2 :-"
پاسخ : سوالات نظریه اعداد هم سطح مرحله دوّم
طبیعی اند؟
a,b صحیح اند ؟؟ اگر صحیح باشند ک خیلی ضایع میشهبه نقل از mehrdad.parsaii :
طبیعی اند؟
ehsan-mokhtarian
کاربر فوقفعال
- ارسالها
- 104
- امتیاز
- 361
- نام مرکز سمپاد
- علامه حلی 1
- شهر
- تهران
- مدال المپیاد
- نقره ریاضی 1391 طلا ریاضی 1392
پاسخ : سوالات نظریه اعداد هم سطح مرحله دوّم
فک کنم می خواستی این سوالو بگی که 15a+16bو 16a-15b مربع هستن. این سوال 4 IMO سال 1996 هست... برای حلش هم می تونید به mathlinks مراجعه کنید...به نقل از mehrdad.parsaii :اعداد طبیعی a,b چنان هستند که اعداد 15a+16b و 16a+15b هر دو مربع کامل هستند. کمترین مقداری که مینیمم این دو مربع کامل میتواند بگیری چند است؟
ویرایش : بله بله درسته حرف شما
ehsan-mokhtarian
کاربر فوقفعال
- ارسالها
- 104
- امتیاز
- 361
- نام مرکز سمپاد
- علامه حلی 1
- شهر
- تهران
- مدال المپیاد
- نقره ریاضی 1391 طلا ریاضی 1392
پاسخ : سوالات نظریه اعداد هم سطح مرحله دوّم
بزار خودت الآن سواله خاصی ندارم...به نقل از mehrdad.parsaii :
Phanntom
کاربر فوقفعال
- ارسالها
- 115
- امتیاز
- 364
- نام مرکز سمپاد
- helli
- شهر
- تهران
- مدال المپیاد
- سابقه دارم!
- دانشگاه
- light massage(پیام نور)
پاسخ : سوالات نظریه اعداد هم سطح مرحله دوّم
صرفا یک معادله سیاله
a(a+1)(a+7)(a+8)=b^2
والا این سوالو خودمم حالیم نمیشه
ولی راه حلش خیلی قشنگه.
سوالای آسونتر تو سطح مرحله 1 تو تاپیک های مربوطه هستش.
چی شد پس؟؟؟؟؟؟
صرفا یک معادله سیاله
a(a+1)(a+7)(a+8)=b^2
والا این سوالو خودمم حالیم نمیشه
ولی راه حلش خیلی قشنگه.
سوالای آسونتر تو سطح مرحله 1 تو تاپیک های مربوطه هستش.
چی شد پس؟؟؟؟؟؟