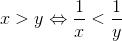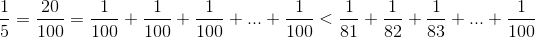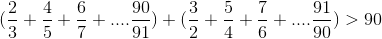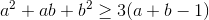- ارسالها
- 512
- امتیاز
- 423
- نام مرکز سمپاد
- شهید سلطانی3کرج
- شهر
- کرج
- سال فارغ التحصیلی
- 1397
- دانشگاه
- politecnico di milano
- رشته دانشگاه
- statistical learning
پاسخ : سوالات ریاضی
دوستان لطفا کمک





1:حاصل را پیدا کنید

2ثابت کنید که:
 عددی گنگ است
عددی گنگ است
3-ثابت کنید که:

دوستان لطفا کمک






1:حاصل را پیدا کنید
2ثابت کنید که:
3-ثابت کنید که: