- ارسالها
- 512
- امتیاز
- 423
- نام مرکز سمپاد
- شهید سلطانی3کرج
- شهر
- کرج
- سال فارغ التحصیلی
- 1397
- دانشگاه
- politecnico di milano
- رشته دانشگاه
- statistical learning
پاسخ : سوالات ریاضی
در هر یک از توابع زیر ثابت کنید تابع در a ناپیوسته است.سپس معین کنید که ناپیوستگی رفع شدنی است یا اساسی.اگر ناپیوستگی رفع شدنی است( f(a را طوری تعریف کنید که ناپیوستگی رفع شود.
=\frac{9x^{2}-4}{3x-2};a=\frac{2}{3})
=[x+2];a=-1)







در هر یک از توابع زیر ثابت کنید تابع در a ناپیوسته است.سپس معین کنید که ناپیوستگی رفع شدنی است یا اساسی.اگر ناپیوستگی رفع شدنی است( f(a را طوری تعریف کنید که ناپیوستگی رفع شود.











 )
)






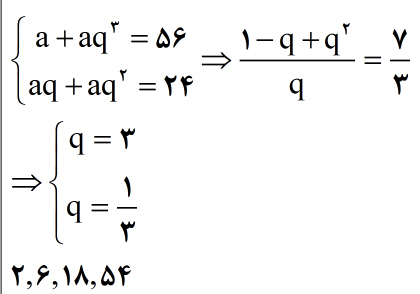

 و
و 

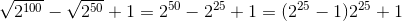
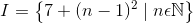
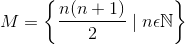
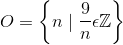
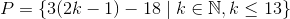
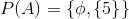
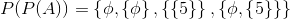

 لطفااااا با بیان شیرین پارسی و به سادگی و روانی یکی توضیح بده
لطفااااا با بیان شیرین پارسی و به سادگی و روانی یکی توضیح بده