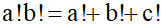- ارسالها
- 1,639
- امتیاز
- 28,325
- نام مرکز سمپاد
- ضروری
- شهر
- ضروری
- سال فارغ التحصیلی
- 0
در بحث فاکتوریل، یکی از زیباترین و چالشیترین سوالات ممکن رو الان دیدم؛ جوابش رو فردا اگر بتونم در شنیدنیهای ریاضی قرار میدم.
تمام a,b,c هایی رو بیابید که:
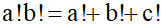
تمام a,b,c هایی رو بیابید که: