- ارسالها
- 571
- امتیاز
- 2,988
- نام مرکز سمپاد
- حلّی ۲
- شهر
- تهران
- سال فارغ التحصیلی
- 1396
- مدال المپیاد
- کامپیوتری بودم
- دانشگاه
- شریف
- رشته دانشگاه
- کامپیوتر
پاسخ : سوالات ترکیبیات
یه شبهه:
سوال 31.1.5 ترکیبیات زرد رو ببینید:
«فرض کنید
 یک عدد گنگ باشد. به ازای هر عدد طبیعی مانند
یک عدد گنگ باشد. به ازای هر عدد طبیعی مانند
 ثابت کنید اعدادی صحیح مانند
ثابت کنید اعدادی صحیح مانند
 و
و
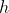 وجود دارند که
وجود دارند که
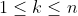 و
و
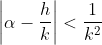 »
»
خب حالا من میگم فرض کنید
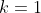 و
و
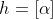 در این صورت حکم مسأله همیشه برقراره
در این صورت حکم مسأله همیشه برقراره
اشکال حرف من چیه؟ اصلا سوال رو درست فهمیدم؟
یه شبهه:
سوال 31.1.5 ترکیبیات زرد رو ببینید:
«فرض کنید
خب حالا من میگم فرض کنید
اشکال حرف من چیه؟ اصلا سوال رو درست فهمیدم؟








 ولی حرف منطقی ای زدی
ولی حرف منطقی ای زدی 

 سورت کردم با Cmp ای که return (first + second) < (second + first))
سورت کردم با Cmp ای که return (first + second) < (second + first))



