You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
المپیاد سوالات ترکیبیات و مباحث ویژه !
- شروع کننده موضوع mahtab.f
- تاریخ شروع
- ارسالها
- 571
- امتیاز
- 2,988
- نام مرکز سمپاد
- حلّی ۲
- شهر
- تهران
- سال فارغ التحصیلی
- 1396
- مدال المپیاد
- کامپیوتری بودم
- دانشگاه
- شریف
- رشته دانشگاه
- کامپیوتر
پاسخ : مسابقه ترکیبیات
جواب رو بگید
منظریم فکر کردن senator77 تموم شهبه نقل از m.m.r :آغا چرا اینجا مگس هم نمیپره؟


X-( X-( X-( X-(
جواب رو بگید
Dark Eagle
کاربر حرفهای

- ارسالها
- 403
- امتیاز
- 660
- نام مرکز سمپاد
- helli 2
- شهر
- Tehran
- مدال المپیاد
- کامپیوتر
پاسخ : مسابقه ترکیبیات
شما سوالاتونو حل کنید هر کسی هم که نمی تونه حل کنه نیاد بگه وایسین من فک کنم !!
خودش یه چند وقت تاپیک رو باز نکنه, هم ساده تره هم به نفع همه اِه ...
این طوری هم تاپیک پیش میره هم اون تا اون موقعی که فک میکنه لازمه می تونه رو سوال فک کنه ...
(اسپمم دیگه نمی دین )
)
شما سوالاتونو حل کنید هر کسی هم که نمی تونه حل کنه نیاد بگه وایسین من فک کنم !!
خودش یه چند وقت تاپیک رو باز نکنه, هم ساده تره هم به نفع همه اِه ...

این طوری هم تاپیک پیش میره هم اون تا اون موقعی که فک میکنه لازمه می تونه رو سوال فک کنه ...
(اسپمم دیگه نمی دین
 )
)- ارسالها
- 571
- امتیاز
- 2,988
- نام مرکز سمپاد
- حلّی ۲
- شهر
- تهران
- سال فارغ التحصیلی
- 1396
- مدال المپیاد
- کامپیوتری بودم
- دانشگاه
- شریف
- رشته دانشگاه
- کامپیوتر
پاسخ : مسابقه ترکیبیات
نکته ی 1: اگر دو یال با نام های u و s به رأس v وصل باشد به طوری که یال (u,v) به سمت u و یال (s,v) به سمت v باشد، در این صورت مسیری به طول 3 وجود دارد که همان svu خواهد بود.
اگر n=2k+1 باشد(یعنی فرد باشد) به این شکل سوال را حل میکنیم.
هر رأس حداقل به k+1 رأس وصل خواهد بود.
پس فرض میکنیم رأس v1، به رئوس v2 تا vk+2 وصل است. فرض میکنیم تمام یال های بین این رئوس و v1 در یک جهت باشند(یا به سمت v1 و یا در جهت عکس آن) چون در غیر این صورت طبق نکته ی 1، مسیری به طول 3 وجود دارد.
حالا رأس v2 را در نظر بگیرید که قرار است به جز v1، به k رأس دیگر وصل شود. اگر به vk+3 تا v2k+1 وصل باشد، در این صورت باید به حداقل یک رأس دیگر وصل شود. آن رأس یکی از رئوس v3 تا vk+2 خواهد بود.
اگر v2 به یکی از رئوس v3 تا vk+2 مثل vi یالی به سمت خودش داشته باشد، در این صورت بسته به جهت رئوس متصل به v1، یکی از دو مسیر viv2v1 و یا v1viv2 مطلوب خواهند بود. اگر چنین یالی، رأسی مثل vi را در جهت عکس v2 به آن وصل کند، یکی از دو مسیر v1v2vi و یا v2viv1 مطلوب خواهند بود.
پس اثبات شد که برای n های فرد، حکم مسأله برقرار است.
برای n=2k، گراف شکل زیر را در نظر بگیرید. (جهت یال های بین لایه ی وسط و لایه ی پایین(!)، به سمت رئوس vk+2 تا v2k است)
در این گراف، درجه ی هر رأس n/2 است و مسیری به طول 3 وجود ندارد.
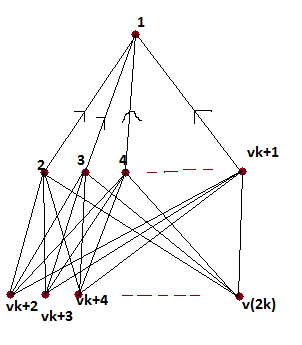
پ.ن: این الآن مثال نقض واسه حکم سوال هست! چرا کسی پاسخگو نیست؟!
اول رفع ابهام: مسیری به طول 3، از 2 یال و 3 رأس تشکیل شده است.به نقل از صبهان :من یه سوال بگم
یه گراف جهت دار داریم که حداقل درجه راس های اون n / 2 ه. ثابت کنید این گراف یه مسیر به طول ۳ داره .
نکته ی 1: اگر دو یال با نام های u و s به رأس v وصل باشد به طوری که یال (u,v) به سمت u و یال (s,v) به سمت v باشد، در این صورت مسیری به طول 3 وجود دارد که همان svu خواهد بود.
اگر n=2k+1 باشد(یعنی فرد باشد) به این شکل سوال را حل میکنیم.
هر رأس حداقل به k+1 رأس وصل خواهد بود.
پس فرض میکنیم رأس v1، به رئوس v2 تا vk+2 وصل است. فرض میکنیم تمام یال های بین این رئوس و v1 در یک جهت باشند(یا به سمت v1 و یا در جهت عکس آن) چون در غیر این صورت طبق نکته ی 1، مسیری به طول 3 وجود دارد.
حالا رأس v2 را در نظر بگیرید که قرار است به جز v1، به k رأس دیگر وصل شود. اگر به vk+3 تا v2k+1 وصل باشد، در این صورت باید به حداقل یک رأس دیگر وصل شود. آن رأس یکی از رئوس v3 تا vk+2 خواهد بود.
اگر v2 به یکی از رئوس v3 تا vk+2 مثل vi یالی به سمت خودش داشته باشد، در این صورت بسته به جهت رئوس متصل به v1، یکی از دو مسیر viv2v1 و یا v1viv2 مطلوب خواهند بود. اگر چنین یالی، رأسی مثل vi را در جهت عکس v2 به آن وصل کند، یکی از دو مسیر v1v2vi و یا v2viv1 مطلوب خواهند بود.
پس اثبات شد که برای n های فرد، حکم مسأله برقرار است.
برای n=2k، گراف شکل زیر را در نظر بگیرید. (جهت یال های بین لایه ی وسط و لایه ی پایین(!)، به سمت رئوس vk+2 تا v2k است)
در این گراف، درجه ی هر رأس n/2 است و مسیری به طول 3 وجود ندارد.

پ.ن: این الآن مثال نقض واسه حکم سوال هست! چرا کسی پاسخگو نیست؟!
daneshvar.amrollahi
کاربر حرفهای

- ارسالها
- 327
- امتیاز
- 130
- نام مرکز سمپاد
- راهنمایی حلی۲/دبیرستان حلی۱۰/دبیرستان علامه طباطبایی
- شهر
- تهران
- سال فارغ التحصیلی
- 1397
- مدال المپیاد
- کامپیوتر
پاسخ : سوالات ترکیبیات
سلام. چندوقت پیش حلی نت بود و تو رده الف یه سوالش اینطوری حل می شد:
به چند طریق می توان اعداد ۱ تا n را در یک ردیف چید به طوری که هر عدد در ردیف، از حداقل نصف اعداد سمت راست خود بزگتر باشد؟
ورودی برنامه: عدد n که میتواند از ۱ تا ۲۰۰۰۰۰ باشد
چجوری حلش کنیم؟
سلام. چندوقت پیش حلی نت بود و تو رده الف یه سوالش اینطوری حل می شد:
به چند طریق می توان اعداد ۱ تا n را در یک ردیف چید به طوری که هر عدد در ردیف، از حداقل نصف اعداد سمت راست خود بزگتر باشد؟
ورودی برنامه: عدد n که میتواند از ۱ تا ۲۰۰۰۰۰ باشد
چجوری حلش کنیم؟
The Smith
کاربر فوقحرفهای

- ارسالها
- 1,061
- امتیاز
- 3,546
- نام مرکز سمپاد
- سلام ایرانزمین
پاسخ : سوالات ترکیبیات
× سوال حل شده ، نمونه ورودی بده ببینم کار میکنه آیا یا نه
سوالش سادس
راهنمایی : رابطه بازگشتی
یه نمونه ی ورودی بده .به نقل از daneshvar.a :سلام. چندوقت پیش حلی نت بود و تو رده الف یه سوالش اینطوری حل می شد:
به چند طریق می توان اعداد ۱ تا n را در یک ردیف چید به طوری که هر عدد در ردیف، از حداقل نصف اعداد سمت راست خود بزگتر باشد؟
ورودی برنامه: عدد n که میتواند از ۱ تا ۲۰۰۰۰۰ باشد
چجوری حلش کنیم؟
× سوال حل شده ، نمونه ورودی بده ببینم کار میکنه آیا یا نه

سوالش سادس
راهنمایی : رابطه بازگشتی
daneshvar.amrollahi
کاربر حرفهای

- ارسالها
- 327
- امتیاز
- 130
- نام مرکز سمپاد
- راهنمایی حلی۲/دبیرستان حلی۱۰/دبیرستان علامه طباطبایی
- شهر
- تهران
- سال فارغ التحصیلی
- 1397
- مدال المپیاد
- کامپیوتر
پاسخ : سوالات ترکیبیات
نمونه ورودی اول: 2 خروجی نمون هاول: 1
نمونه ورودی دوم: 5 خروجی نمونه دوم: 12
نمونه ورودی سوم: 6 خروجی نمونه سوم: 36
اگر درست حل کردید، بگید رابطه رو چجوری به دست آوردید. اصلش همونه. چون با چاپ باقی مانده جواب بر 1e9+7 میشه جواب رو ساده کرد.
میگید بازگشتیه یعنی باید n رو کوچیک کنیم دیگه؟ خوب چجوری میشه؟ یعنی از رو کوچک تر ها چجوری بزگرتره رو پیدا کنیم...
نمونه ورودی اول: 2 خروجی نمون هاول: 1
نمونه ورودی دوم: 5 خروجی نمونه دوم: 12
نمونه ورودی سوم: 6 خروجی نمونه سوم: 36
اگر درست حل کردید، بگید رابطه رو چجوری به دست آوردید. اصلش همونه. چون با چاپ باقی مانده جواب بر 1e9+7 میشه جواب رو ساده کرد.
میگید بازگشتیه یعنی باید n رو کوچیک کنیم دیگه؟ خوب چجوری میشه؟ یعنی از رو کوچک تر ها چجوری بزگرتره رو پیدا کنیم...
The Smith
کاربر فوقحرفهای

- ارسالها
- 1,061
- امتیاز
- 3,546
- نام مرکز سمپاد
- سلام ایرانزمین
پاسخ : سوالات ترکیبیات

این عدد یکی مونده به آخر
از چند تا عدد باید بزرگتر باشه ؟ ۱دونه یا هیچی ؟
ینی اگه فرد تا عدد سمت راستش بود ، از سقف نصفشون بیشتر باشه یا کف نصفشون ؟
فقط یه مشکلی هستبه نقل از daneshvar.a :نمونه ورودی اول: 2 خروجی نمون هاول: 1
نمونه ورودی دوم: 5 خروجی نمونه دوم: 12
نمونه ورودی سوم: 6 خروجی نمونه سوم: 36
اگر درست حل کردید، بگید رابطه رو چجوری به دست آوردید. اصلش همونه. چون با چاپ باقی مانده جواب بر 1e9+7 میشه جواب رو ساده کرد.
میگید بازگشتیه یعنی باید n رو کوچیک کنیم دیگه؟ خوب چجوری میشه؟ یعنی از رو کوچک تر ها چجوری بزگرتره رو پیدا کنیم...

این عدد یکی مونده به آخر
از چند تا عدد باید بزرگتر باشه ؟ ۱دونه یا هیچی ؟
ینی اگه فرد تا عدد سمت راستش بود ، از سقف نصفشون بیشتر باشه یا کف نصفشون ؟
daneshvar.amrollahi
کاربر حرفهای

- ارسالها
- 327
- امتیاز
- 130
- نام مرکز سمپاد
- راهنمایی حلی۲/دبیرستان حلی۱۰/دبیرستان علامه طباطبایی
- شهر
- تهران
- سال فارغ التحصیلی
- 1397
- مدال المپیاد
- کامپیوتر
پاسخ : سوالات ترکیبیات
عدد یکی مونده به آخر تو موقعیت دوم قرار داره. پس باید از حداقل یکی از قبلیاش که اولی هستش، بیشتر باشه. شماره ها از 1 تا N هستند نه 0 تا n-1. فقط عدد آخر میتونه هرچی باشه چون باید از 0/2 بیشتر باشه که میشه صفر.
کف سمت راستش. اگر زوج بود که دقیقا باید از i/2 سمت راستش بیشتر باشه. اگر هم فرد بود همون i/2 تو سی پلاس پلاس جواب میده چون کف میگیره فکر کنم. یعنی مثلا اگر نفر پتجم باشه، باید حداقل از 2 نفر بیشتر باشه.به نقل از صبهان :فقط یه مشکلی هست
این عدد یکی مونده به آخر
از چند تا عدد باید بزرگتر باشه ؟ ۱دونه یا هیچی ؟
ینی اگه فرد تا عدد سمت راستش بود ، از سقف نصفشون بیشتر باشه یا کف نصفشون ؟
عدد یکی مونده به آخر تو موقعیت دوم قرار داره. پس باید از حداقل یکی از قبلیاش که اولی هستش، بیشتر باشه. شماره ها از 1 تا N هستند نه 0 تا n-1. فقط عدد آخر میتونه هرچی باشه چون باید از 0/2 بیشتر باشه که میشه صفر.
The Smith
کاربر فوقحرفهای

- ارسالها
- 1,061
- امتیاز
- 3,546
- نام مرکز سمپاد
- سلام ایرانزمین
پاسخ : سوالات ترکیبیات
خروجی اول باید جوابش بشه ۲. نه ۱
طبق حرف توبه نقل از daneshvar.a :کف سمت راستش. اگر زوج بود که دقیقا باید از i/2 سمت راستش بیشتر باشه. اگر هم فرد بود همون i/2 تو سی پلاس پلاس جواب میده چون کف میگیره فکر کنم. یعنی مثلا اگر نفر پتجم باشه، باید حداقل از 2 نفر بیشتر باشه.
عدد یکی مونده به آخر تو موقعیت دوم قرار داره. پس باید از حداقل یکی از قبلیاش که اولی هستش، بیشتر باشه. شماره ها از 1 تا N هستند نه 0 تا n-1. فقط عدد آخر میتونه هرچی باشه چون باید از 0/2 بیشتر باشه که میشه صفر.
خروجی اول باید جوابش بشه ۲. نه ۱
daneshvar.amrollahi
کاربر حرفهای

- ارسالها
- 327
- امتیاز
- 130
- نام مرکز سمپاد
- راهنمایی حلی۲/دبیرستان حلی۱۰/دبیرستان علامه طباطبایی
- شهر
- تهران
- سال فارغ التحصیلی
- 1397
- مدال المپیاد
- کامپیوتر
پاسخ : سوالات ترکیبیات
صورت سوالی که من دارم نگفته کف یا سقف. ولی چون تست کیس خود سوال با ورودی نمونه ۲، جواب ۱ رو داده، پس احتمالا باید سقف منظورش باشه. یعنی مثال ۲ ۱ غلط بشه. که سقف یک دوم بشه ۱ و نفر دوم نتونسته باشه از ۱ نفر قبلی خود بهتر باشه.به نقل از صبهان :طبق حرف تو
خروجی اول باید جوابش بشه ۲. نه ۱
daneshvar.amrollahi
کاربر حرفهای

- ارسالها
- 327
- امتیاز
- 130
- نام مرکز سمپاد
- راهنمایی حلی۲/دبیرستان حلی۱۰/دبیرستان علامه طباطبایی
- شهر
- تهران
- سال فارغ التحصیلی
- 1397
- مدال المپیاد
- کامپیوتر
پاسخ : سوالات ترکیبیات
کدش خیلی اهمیت نداره. بیشتر همون راه حلشه. اصلا فرض کتیم به جای n عدد ۵ گذاشتیم و میخوایم سوال ترکیبیات حل کنیم...
مثال ورودی و خروجی بیشتر بذارم؟
من تست کیس ۳ رو اطمینان خیلی خیلی کامل ندارم ولی چون با کدی که اکسپت گرفته، اون خروجی رو میده گذاشتم. یه رابطه براش زده ولی نمی دونم چجوری بهش رسیده...به نقل از صبهان :دارم سعی میکنم حلش کنم.
دو تا راه حل دارم که یکیش برای یه سریش درست جواب میده
یکیش برای یه سری دیگع
کدش خیلی اهمیت نداره. بیشتر همون راه حلشه. اصلا فرض کتیم به جای n عدد ۵ گذاشتیم و میخوایم سوال ترکیبیات حل کنیم...
مثال ورودی و خروجی بیشتر بذارم؟
The Smith
کاربر فوقحرفهای

- ارسالها
- 1,061
- امتیاز
- 3,546
- نام مرکز سمپاد
- سلام ایرانزمین
پاسخ : سوالات ترکیبیات
رابطه :

اثباتش رو مطمعن نیستم اصلا.
ولی
توی جایگاه آخر همیشه ۱ هست، چون کوچکترین عدده.
و عدد ۲ هم یا توی خونه ی آخره یا یکی مونده به آخر.
و توی جایگاه اول و دوم ، همیشه عددای بزرگتر مساوی سقف n / 2.
چون اگه غیر از این باشه ، یه عدد کوچیک تر از اون توی خونه ی اول و دوم قرار بگیره ، حتما از نصف اعداد بعدش بزرگتر نیست (چون نصف عددا بزرگتر از n / 2 هستن.)
جایگاه اول رو در نظر نگیر، میشه An-1 و برای اولین خونه هم سقف n / 2 حالت داریم که میشه فرمولی که دادم.
ینی Ai = Ai-1 * n/2 :)
رابطه :

اثباتش رو مطمعن نیستم اصلا.
ولی
توی جایگاه آخر همیشه ۱ هست، چون کوچکترین عدده.
و عدد ۲ هم یا توی خونه ی آخره یا یکی مونده به آخر.
و توی جایگاه اول و دوم ، همیشه عددای بزرگتر مساوی سقف n / 2.
چون اگه غیر از این باشه ، یه عدد کوچیک تر از اون توی خونه ی اول و دوم قرار بگیره ، حتما از نصف اعداد بعدش بزرگتر نیست (چون نصف عددا بزرگتر از n / 2 هستن.)
جایگاه اول رو در نظر نگیر، میشه An-1 و برای اولین خونه هم سقف n / 2 حالت داریم که میشه فرمولی که دادم.
ینی Ai = Ai-1 * n/2 :)
daneshvar.amrollahi
کاربر حرفهای

- ارسالها
- 327
- امتیاز
- 130
- نام مرکز سمپاد
- راهنمایی حلی۲/دبیرستان حلی۱۰/دبیرستان علامه طباطبایی
- شهر
- تهران
- سال فارغ التحصیلی
- 1397
- مدال المپیاد
- کامپیوتر
پاسخ : سوالات ترکیبیات

یک کم فکر می کنم بعد دوباره یه پاسخ خواهم گذاشتبه نقل از صبهان :رابطه :
اثباتش رو مطمعن نیستم اصلا.
ولی
توی جایگاه آخر همیشه ۱ هست، چون کوچکترین عدده.
و عدد ۲ هم یا توی خونه ی آخره یا یکی مونده به آخر.
و توی جایگاه اول و دوم ، همیشه عددای بزرگتر مساوی سقف n / 2.
چون اگه غیر از این باشه ، یه عدد کوچیک تر از اون توی خونه ی اول و دوم قرار بگیره ، حتما از نصف اعداد بعدش بزرگتر نیست (چون نصف عددا بزرگتر از n / 2 هستن.)
جایگاه اول رو در نظر نگیر، میشه An-1 و برای اولین خونه هم سقف n / 2 حالت داریم که میشه فرمولی که دادم.
ینی Ai = Ai-1 * n/2 :)

kavian77
کاربر جدید

- ارسالها
- 3
- امتیاز
- 0
- نام مرکز سمپاد
- شهید سلطانی 3
- شهر
- کرج
پاسخ : مسابقه ترکیبیات
دوستان نیازی نیست انقدر خودتون رو اذیت کنید .
هر پله ی n*n با یک مربع n-1*n-1 و دو مربع 1*1 پر میشه .
در واقع کمینه جواب 3 می شود .
موفق و سلامت باشید
نظر شخصی ام بود اگه اشتباه کردم خوشحال میشم بفرمائید .
سلام به همگیبه نقل از mhjh :من چون خودم سوالو تازه فهمیدم ، الآن برات توضیح میدم . سوال میگه یه شکلی که شبیه پله است رو چجوری میشه به مربع هایی افراز کرد . (کمترین مربع )
یعنی این مربع ها فقط 2*2 نیستند ، 1*1 و 3*3 و ... هم میتونن باشن .
[]
دوستان نیازی نیست انقدر خودتون رو اذیت کنید .
هر پله ی n*n با یک مربع n-1*n-1 و دو مربع 1*1 پر میشه .
در واقع کمینه جواب 3 می شود .
موفق و سلامت باشید
نظر شخصی ام بود اگه اشتباه کردم خوشحال میشم بفرمائید .








