پله ی n تایی:به نقل از kavian77 :
آآآآ ببخشیدبه نقل از amoo.majid :پله ی n تایی:
ممنون که دارید روی سوال فکر میکنید اما تقریبا همه ی اینا رو بچه ها گفتن(آخر سر هم به به سری حالت استثنا رسیدیم و حل این سوال رو به وقتی که یه نفر یه چیز تازه به ذهنش برسه موکول کردیم) و الآن باید روی سوال زیر فکر کنیم.به نقل از kavian77 :
دوستان به هیچ وجه علاقه ای به فرستادن اسپم ندارم . ولی بهتر بود با جوابی که 2 ساعت روش فکر شده بهتر از اینها برخورد بشه نه حداقل با شخص من .به نقل از amoo.majid :
این فرمول صریحشه ، من بازگشتی حل کردمبه نقل از daneshvar.a :
فرض کنید بخواهیم k شیء از اشیای متمایز برداریم؛ بدین ترتیب، باید n-k شیء از اشیای یکسان برداریم و برای چنین انتخابی (C(2n+1, k حالت داریم. (چون باید k شیء از 2n+1 شیء متمایز انتخاب کنیم و از طرفی با توجه به این که n شی یکسان هستند، برای انتخاب n-k شء دیگر، 1 حالت داریم)به نقل از ـفــاتـــــ :
قبول داری دوتا اسب فقط میتونن به صورت L هم دیگه رو تهدید کنن؟حالا شکل L چیه؟ببین تو هر مستطیل دو در سه انتخاب کنی دقیقا 4 تا حالت داره برا تهدید اینم که درکش اسونه؟به نقل از TheBest444 :
حداقل وقتی سوال رو از آزمون گراف امسال می گی سوالو درست بگوبه نقل از ๖ۣۜTango :توران (طوران) ... نمیدونم کدومش درسته
کایت : گراف 4 راسی بدون کامل یه یال کم !
ثابت کنید تعداد یال های یک گراف بدون کایت بین 9n^2 و 12n^2 است ...
قبل از همه چیز تعریف میکنیم Fn یعنی تعداد راه های پرانتزگذاری یک عبارت که شامل n متغیر هست. واضحه که F1=1 و F2=1 و F3=2به نقل از ـفاتــــ :
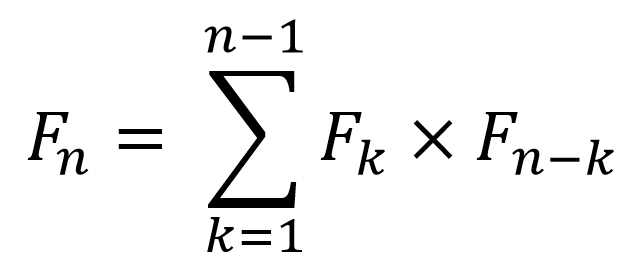
یه جورایی نصفش غلط بودبه نقل از مهسا.ق :حداقل وقتی سوال رو از آزمون گراف امسال می گی سوالو درست بگو
چیزی که از سوال جا افتاده اینه که گراف 6n راسی هست!
... درستش کردم ...
باسه حل این سوال بروت فورس(کلمه ی بهتری به ذهنم نرسید) زدم، اگه راه بهتری هست بگیدبه نقل از TheBest444 :
