rezaezio
کاربر فوقحرفهای

- ارسالها
- 1,167
- امتیاز
- 1,956
- نام مرکز سمپاد
- حلّیِ 2
- شهر
- تهران
- مدال المپیاد
- برنز و طلای کامپیوتر !
- دانشگاه
- شریف
- رشته دانشگاه
- نرم افزار
پاسخ : سوالات گراف
1.1.12) نشان دهید گراف پترسن دو بخشی است ، سایز بزرگترین مجموعه مستقل را پیدا کنید.
پاسخ :
گراف پترسن دو بخشی نیست ، چون دور با طول فرد داره
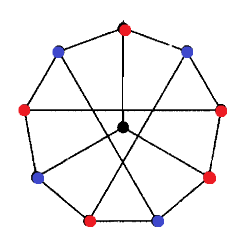
بزرگترین زیر مجموعه مستقل گراف پترسن 4 عضو داره
اثبات اینکه از 4 بیشتر نمیشه :
اگر راس سبز در شکل زیر در مجموعه مستقل باشه ؛ آنگاه بقیه عضو های مجموعه باید از بین عضو های درون دایره های قرمز در شکل زیر انتخاب بشن و چون از هر دایره حداکثر 1 عضو را می توان انتخاب کرد ، 4=3+1 عضو انتخاب شده است.
اگر راس سبز در مجموعه مستقل نیاید ؛ آنگاه دوری به طول 9 داریم که بدیهی است از دوری به طول 9 برای قرار گرفتن در مجموعه مستقل حداکثر میتوان 4 عضو را انتخاب کرد.
شکل زیر هم مثالی برای 4 راس
1.1.13)نشان دهید که گراف k مکعب دو بخشی است .
پاسخ :
ثابت می کتم این گراف دور به طول فرد نداره و از این حرف میشه نتیجه گرفت که دو بخشیه
در گراف k مکعب هر راس با راس های مجاورش از نظر زوجیت تعداد یک ها متفاوت است پس پس اگر دور با شروع از راس A باشد چون پایانش هم راس A هست ؛ پس باید زوج بار تغییر زوجیت بدیم ، پس طول دور ما زوج است. (می دونم که بد توضیح دادم )
)
1.1.14) ثابت کنید که با حذف کردن مربع های گوشه و رو به رو ( به نظرم منظورش مربع گوشه بالا و چپ و مربع گوشه پایین و راست هست ) از یک جدول شطرنجی 8 در 8 ، تخته ای به دست می آید که نمی توان آن را با دومینو پوشاند.این مساله را با استفاده از گراف های دو بخشی تعمیم دهید.
پاسخ :
نمیتوان زیرا 30 خانه با رنگ سیاه و 32 مهره با رنگ سفید داریم و هر دومینو یک خانه سفید و یک خانه سیاه را می پوشاند.
در حالت کلی اگر با حذف تعدادی خانه بتوان جدول را با دومینو پر کرد ؛ آنگاه تعداد خانه های سیاه حذف شده برابر با تعداد خانه های سفید حذف شده است.
1.1.15) چهار خانواده رو به رو در گراف را در نظر بگیرید. A = { مسیر ها } , B = { دور ها } , C = { خوشه ها } , D = { گراف های دو بخشی } . برای هر جفت از این خانواده ها ، کلاس های یکریختی که هر دو خانواده را شامل می شوند را تعیین کنید. ( خودم هم نفهمیدم )
)
1.1.16)یکریخت بودن شکل های زیر را بررسی کنید.
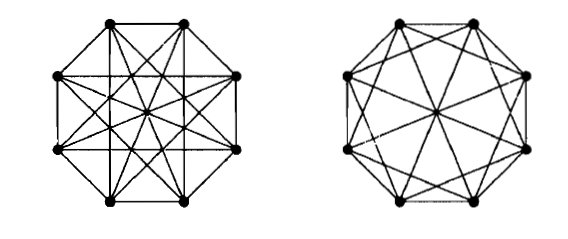
پاسخ :
یکریخت نیستند زیرا اگر گراف های مکمل آن ها را در نظر بگیریم یکی از دوری به طول 8 تشکیل شده است و دیگری از دو دور به طول 4
1.1.17)تعداد زده های یکریختی گرافی با 7 راس که درجه هر راس آن 4 است را بدست آورید.
پاسخ :
گراف مکمل این گراف را در نظر می گیریم ، چون درجه هر راس در این جا 2 است پس حتما از دور تشکیل شده است و با بررسی می فهمیم که یا دوری به طول 7 است و یا اینکه دو دور به طول های 3 و 4
1.1.18) بررسی کنید که کدامین جفت های زیر یکریخت هستند.
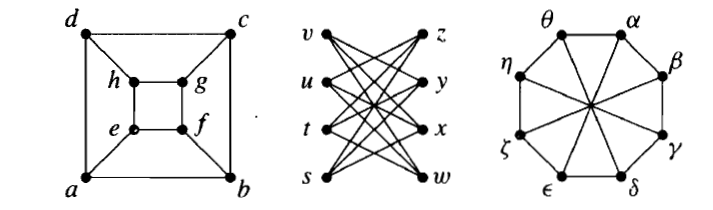
پاسخ :
سمت راست ترین گراف دو بخشی نیست چون دور به طول فرد داره ولی گراف وسط و گراف سمت چپ یکریخت هستند .
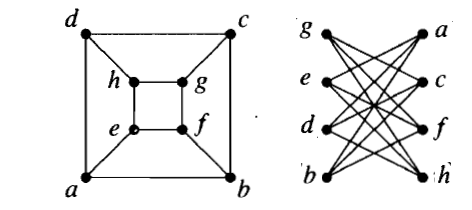
1.1.19) بررسی کنید که کدامین جفت های زیر یکریخت هستند.
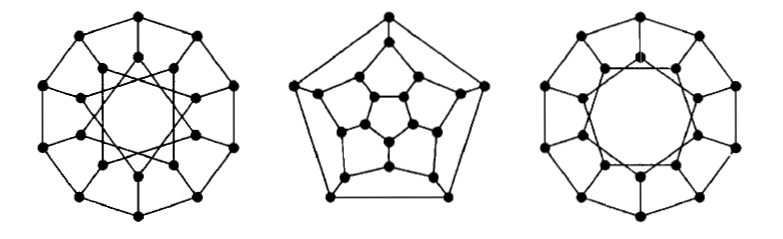
پاسخ :
گراف سمت چپ دو بخشی است ولی گراف های وسط و گراف سمت راست دور به طول فرد دارند.
گراف سمت راست و وسط با هم یکریخت هستند.
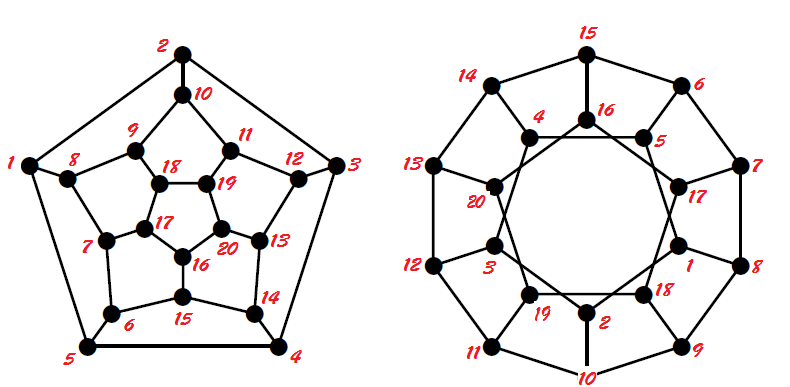
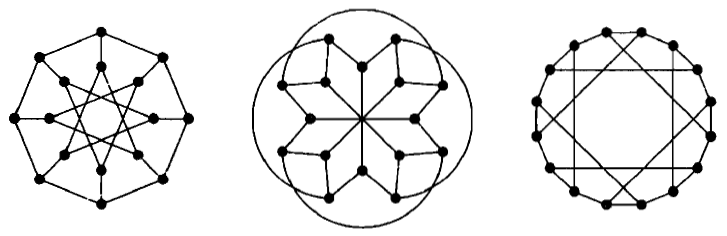
1.1.20) بررسی کنید که کدامین جفت های زیر یکریخت هستند.
پاسخ :
گراف وسط دور با طول فرد داره پس دوبخشی نیست ولی گراف های راست و چپ دو بخشی هستند.
همچنین گراف های چپ و وسط یکریخت هستند.
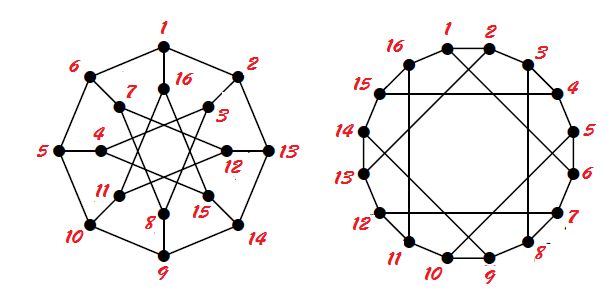
1.1.21) دو بخشی بودن و یک ریخت بودن گراف های زیر را بررسی کنید.
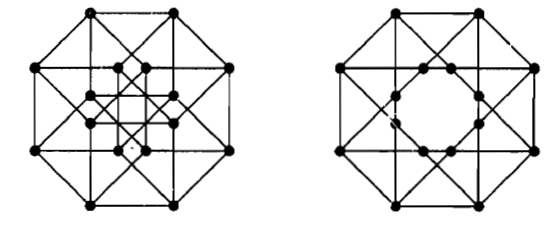
1.1.22) تعیین کنید کدام یک از جفت های زیر یکریخت هستند ، اثباتی ارائه دهید که در آن کمترین تعداد ممکن آزمایش را انجام داده باشید.

پاسخ :
گراف مکمل هر کدام از 5 گراف را رسم می کنیم ، گراف ها را از چپ به راست با شماره های 1 تا 5 نامگذاری می کنیم ،
متمم گراف های 1 و 2 و 5 دوری به طول 7 هستند ولی مکمل گراف های 3 و 4 دو دور به طول های 3 و 4 هستند. پس گراف های 1 و 2 و 5 با هم پیکریخت هستند و گراف های 3 و 4 با هم.
1.1.23 ) در هر کلاس رده زیر ؛ کوچک ترین n را چنان بیابید که حداقل 2 گراف با مجموعه درجات یکسان با n راس داشته باشیم که یکریخت نباشند.
1- همه ی گراف ها 2- گراف های بدون طوقه ( لوپ ) 3- گراف های ساده
پ.ن) در ضمن اینا سوال های آسونش بودن ، واسه اینکه این جا مرجع هست جوابا رو پشت هم نوشتم تا به سوالات نسبتا جون دارش برسیم !
پ.ن 2) به درخواست تعداد زیادی از کاربران سایت از جمله علیرضا پاسخ ها رو سفید کردم که ملت خودشون فکر کنند ! در ضمن عکس ها سفید نمیشن ملت از جمله علیرضا مواظب چشماشون باشند
ملت از جمله علیرضا مواظب چشماشون باشند
1.1.12) نشان دهید گراف پترسن دو بخشی است ، سایز بزرگترین مجموعه مستقل را پیدا کنید.
پاسخ :
گراف پترسن دو بخشی نیست ، چون دور با طول فرد داره

بزرگترین زیر مجموعه مستقل گراف پترسن 4 عضو داره
اثبات اینکه از 4 بیشتر نمیشه :
اگر راس سبز در شکل زیر در مجموعه مستقل باشه ؛ آنگاه بقیه عضو های مجموعه باید از بین عضو های درون دایره های قرمز در شکل زیر انتخاب بشن و چون از هر دایره حداکثر 1 عضو را می توان انتخاب کرد ، 4=3+1 عضو انتخاب شده است.
اگر راس سبز در مجموعه مستقل نیاید ؛ آنگاه دوری به طول 9 داریم که بدیهی است از دوری به طول 9 برای قرار گرفتن در مجموعه مستقل حداکثر میتوان 4 عضو را انتخاب کرد.

شکل زیر هم مثالی برای 4 راس

1.1.13)نشان دهید که گراف k مکعب دو بخشی است .
پاسخ :
ثابت می کتم این گراف دور به طول فرد نداره و از این حرف میشه نتیجه گرفت که دو بخشیه
در گراف k مکعب هر راس با راس های مجاورش از نظر زوجیت تعداد یک ها متفاوت است پس پس اگر دور با شروع از راس A باشد چون پایانش هم راس A هست ؛ پس باید زوج بار تغییر زوجیت بدیم ، پس طول دور ما زوج است. (می دونم که بد توضیح دادم
 )
)1.1.14) ثابت کنید که با حذف کردن مربع های گوشه و رو به رو ( به نظرم منظورش مربع گوشه بالا و چپ و مربع گوشه پایین و راست هست ) از یک جدول شطرنجی 8 در 8 ، تخته ای به دست می آید که نمی توان آن را با دومینو پوشاند.این مساله را با استفاده از گراف های دو بخشی تعمیم دهید.
پاسخ :
نمیتوان زیرا 30 خانه با رنگ سیاه و 32 مهره با رنگ سفید داریم و هر دومینو یک خانه سفید و یک خانه سیاه را می پوشاند.
در حالت کلی اگر با حذف تعدادی خانه بتوان جدول را با دومینو پر کرد ؛ آنگاه تعداد خانه های سیاه حذف شده برابر با تعداد خانه های سفید حذف شده است.
1.1.15) چهار خانواده رو به رو در گراف را در نظر بگیرید. A = { مسیر ها } , B = { دور ها } , C = { خوشه ها } , D = { گراف های دو بخشی } . برای هر جفت از این خانواده ها ، کلاس های یکریختی که هر دو خانواده را شامل می شوند را تعیین کنید. ( خودم هم نفهمیدم
 )
) 1.1.16)یکریخت بودن شکل های زیر را بررسی کنید.

پاسخ :
یکریخت نیستند زیرا اگر گراف های مکمل آن ها را در نظر بگیریم یکی از دوری به طول 8 تشکیل شده است و دیگری از دو دور به طول 4
1.1.17)تعداد زده های یکریختی گرافی با 7 راس که درجه هر راس آن 4 است را بدست آورید.
پاسخ :
گراف مکمل این گراف را در نظر می گیریم ، چون درجه هر راس در این جا 2 است پس حتما از دور تشکیل شده است و با بررسی می فهمیم که یا دوری به طول 7 است و یا اینکه دو دور به طول های 3 و 4
1.1.18) بررسی کنید که کدامین جفت های زیر یکریخت هستند.

پاسخ :
سمت راست ترین گراف دو بخشی نیست چون دور به طول فرد داره ولی گراف وسط و گراف سمت چپ یکریخت هستند .

1.1.19) بررسی کنید که کدامین جفت های زیر یکریخت هستند.

پاسخ :
گراف سمت چپ دو بخشی است ولی گراف های وسط و گراف سمت راست دور به طول فرد دارند.
گراف سمت راست و وسط با هم یکریخت هستند.

1.1.20) بررسی کنید که کدامین جفت های زیر یکریخت هستند.

پاسخ :
گراف وسط دور با طول فرد داره پس دوبخشی نیست ولی گراف های راست و چپ دو بخشی هستند.
همچنین گراف های چپ و وسط یکریخت هستند.

1.1.21) دو بخشی بودن و یک ریخت بودن گراف های زیر را بررسی کنید.

1.1.22) تعیین کنید کدام یک از جفت های زیر یکریخت هستند ، اثباتی ارائه دهید که در آن کمترین تعداد ممکن آزمایش را انجام داده باشید.

پاسخ :
گراف مکمل هر کدام از 5 گراف را رسم می کنیم ، گراف ها را از چپ به راست با شماره های 1 تا 5 نامگذاری می کنیم ،
متمم گراف های 1 و 2 و 5 دوری به طول 7 هستند ولی مکمل گراف های 3 و 4 دو دور به طول های 3 و 4 هستند. پس گراف های 1 و 2 و 5 با هم پیکریخت هستند و گراف های 3 و 4 با هم.
1.1.23 ) در هر کلاس رده زیر ؛ کوچک ترین n را چنان بیابید که حداقل 2 گراف با مجموعه درجات یکسان با n راس داشته باشیم که یکریخت نباشند.
1- همه ی گراف ها 2- گراف های بدون طوقه ( لوپ ) 3- گراف های ساده
پ.ن) در ضمن اینا سوال های آسونش بودن ، واسه اینکه این جا مرجع هست جوابا رو پشت هم نوشتم تا به سوالات نسبتا جون دارش برسیم !
پ.ن 2) به درخواست تعداد زیادی از کاربران سایت از جمله علیرضا پاسخ ها رو سفید کردم که ملت خودشون فکر کنند ! در ضمن عکس ها سفید نمیشن
 ملت از جمله علیرضا مواظب چشماشون باشند
ملت از جمله علیرضا مواظب چشماشون باشند
















