rezaezio
کاربر فوقحرفهای

- ارسالها
- 1,167
- امتیاز
- 1,956
- نام مرکز سمپاد
- حلّیِ 2
- شهر
- تهران
- مدال المپیاد
- برنز و طلای کامپیوتر !
- دانشگاه
- شریف
- رشته دانشگاه
- نرم افزار
پاسخ : سوالات گراف
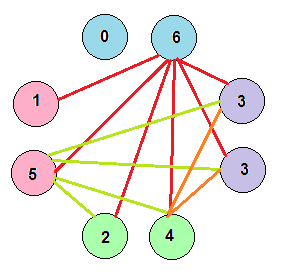
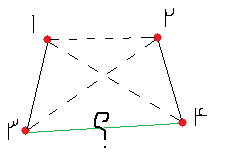
یک تورنمنت n راسی داریم، یال ها رو با دو رنگ آبی و قرمز رنگ کرده ایم، ثابت کنید یک راس هست که به بقیه رئوس مسیر تکرنگ داره.
یک تورنمنت n راسی داریم، یال ها رو با دو رنگ آبی و قرمز رنگ کرده ایم، ثابت کنید یک راس هست که به بقیه رئوس مسیر تکرنگ داره.