Moshk
کاربر فوق‌حرفه‌ای
- ارسالها
- 1,141
- امتیاز
- 2,882
- نام مرکز سمپاد
- شهید بهشتی 1
- شهر
- ساری
- سال فارغ التحصیلی
- 1397
پاسخ : سوالات ریاضی
ازین ببعد یادم باشه از یه دهه هشتادی ادعا چیزی نپرسم
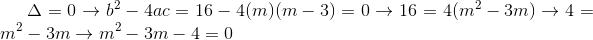
خب الان ما به یه معادله دو مجهولی بر حسب m دست پیدا کردیم که ریشه هاش اون چیزین که سوال میخاد:
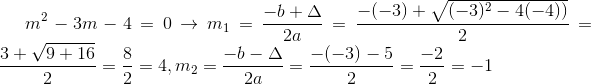
که دوتا جواب ام مساوی 4 و -1 در میاد ازش:
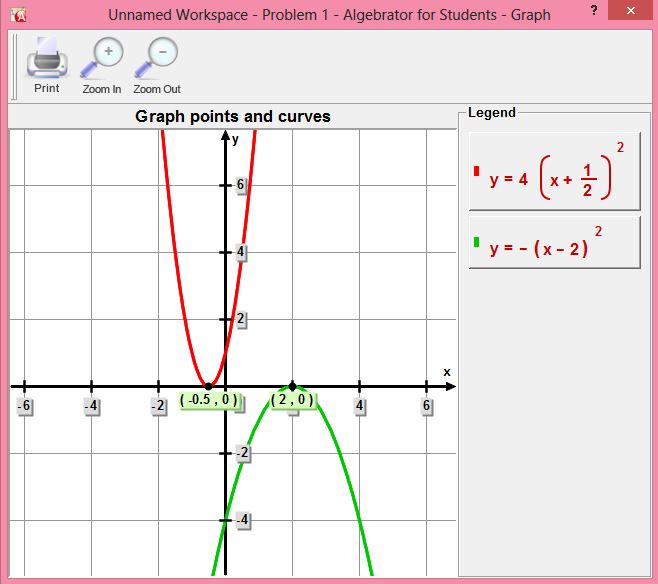
تابع های موجودشم میشن(که قرمز m=4 و سبز m=-1 هست):
واقعا ممنونمبه نقل از Farzin2x :واقعا نمیدونی؟
حالا دیگه کار از کار گذشت خوبه گفت زود جواب بدین
معادله پارامتری بجای عدد پارامتر داره
ازین ببعد یادم باشه از یه دهه هشتادی ادعا چیزی نپرسم
وقتی میگه مماسه یعنی باید یه ریشه مضاعف داشته باشه: تو تابع درجه دو ax^2+bx+c ، باید دلتا (رادیکال b^2-4ac) برابر 0 باشه پس رادیکال دلتا هم صفره یعنی b^2-4ac هم صفره:به نقل از .saghar :
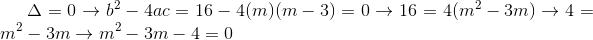
خب الان ما به یه معادله دو مجهولی بر حسب m دست پیدا کردیم که ریشه هاش اون چیزین که سوال میخاد:
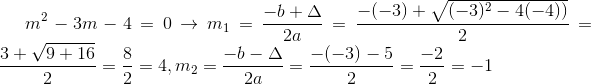
که دوتا جواب ام مساوی 4 و -1 در میاد ازش:
تابع های موجودشم میشن(که قرمز m=4 و سبز m=-1 هست):
)) منتظر جواب کوتاهم 
