پاسخ : آرشیو سوالات از گذشته تا کنون
اِهِم!!!

راه OOOWNING درسته... فقط چند تا جاش جوب داره! من کاملشو مینویسم با اجازه.

اول فرض میکنیم x , y هر دو نامنفی هستن! در این صورت:
x + y <= 100 ; 0 <= x , y <= 100
خب! الان تعداد این زوج مرتب ها رو چجوری میشماریم؟!
یه ایدهی خوب اینه: ???
x + y + t = 100 ; 0 <= x , y , t <= 100
حالا تعداد اینو دیگه راحت میشماریم:
(ترکیب 2 از 102)
همونطور که OOOWNING گفت؛ باید اینو در چهار هم ضرب کنیم. چون هر کدوم از x , y دو حالت دارن: مثبت و منفی
حالا اگه دقت کنید، میبینید که این دو زوج مرتب هیچ فرقی با هم ندارن... ولی ما دو بار شمردیمشون!

(16+ , 0-)
(16+ , 0+)
پس باید اینا رو کم کنیم:
اگه x=0 باشه؛ y میتونه 200 حالت داشته باشه!(فعلاً 0 رو در نظر نگیرین)
به طور مشابه برای y=0 .
اگر هم هر دو 0 بودند 3تا حالت زیادتر شمردیم!
پس در کل:
3 - 200 - 200 - ((انتخاب 2 از 102)) * 4
20201 =
اون چیزی که روژین خانم گفت رو درست نفهمیدم دقیقاً

... ولی فک کنم منظورش این بود:

اگه x=100 باشه؛ y میتونه 1 حالت داشته باشه {0}.
اگه x=99 باشه؛ y میتونه 3 حالت داشته باشه {1 و 0 و 1-}
اگه x=98 باشه؛ y میتونه 5 حالت داشته باشه {2 و 1 و 0 و 1- و 2-}
...
اگه یکم فک کنید، میفهمید چرا؟!! پس جواب برابره با:


که این هم همون 20201 میشه!
پ.ن: اگه جاییش رو متوجه نشدید، در خدمتم!

پ.پ.ن: اگه راه دیگهای بود، استقبال میکنیم!!!







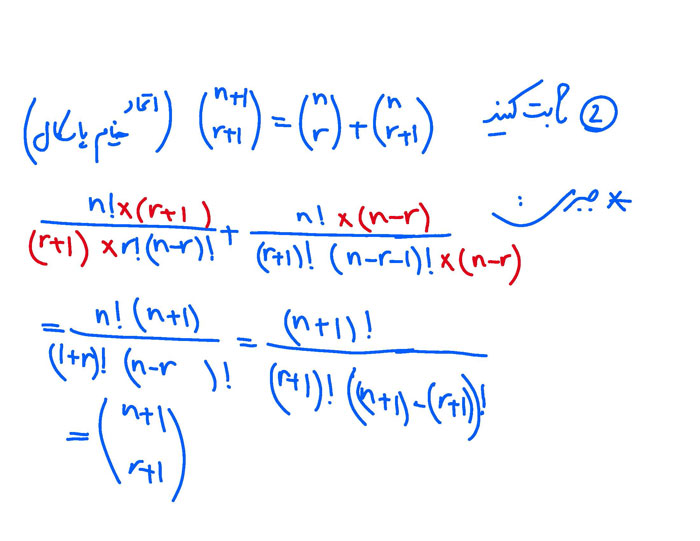
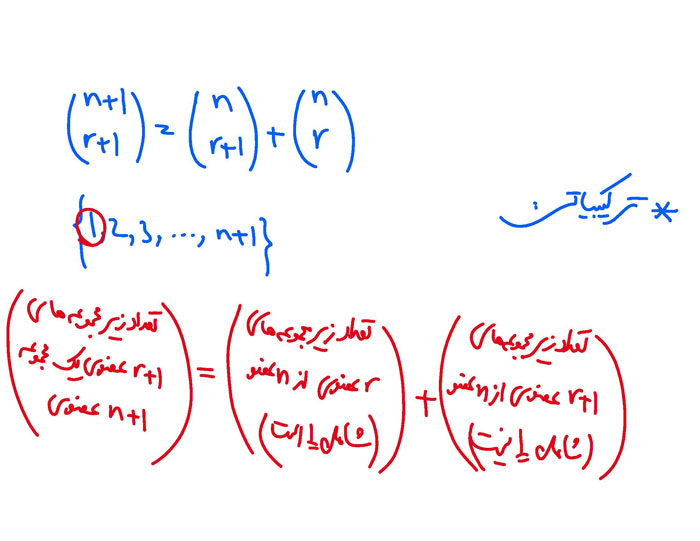



 ... ولی فک کنم منظورش این بود:
... ولی فک کنم منظورش این بود:




 نمیدونم شاید منم زیادی خوابم میاد (
نمیدونم شاید منم زیادی خوابم میاد (





