سوالات ریاضی

[Apar]

جوابش یک میشه؟

1 میشه که این یک مورد و سوال معروفه،ولی اثبات چیه؟
البته تقریبا 1 میشه نه دقیقا چون پی تو رابطه هست

 

[دژاوو]

سلام کسی می‌تونه توی این سوال کمک کنه؟!

اول باید یک مسئله یِ کوچکتر رو برای رسیدن به جواب حل کرد؛ باید مجموعِ مساحتِ این چهار تا مربع رو به دست بیاریم:
https://www.geogebra.org/m/kyte3gpfدر اینجا به صورت دستی می تونیم مربع ها رو جابه‌جا کنیم و ببینیم که در هر حالت، مجموعِ مساحتِ اون ها یکسان خواهد بود.
https://www.desmos.com/calculator/iet6hp60fiاگر در این سایت هم به بخش areas و زیر مجموعه یِ A Total نگاه کنیم، باز مساحتِ کل با جابه‌جایی عوض نمیشه.
این قضیه به طور کلی به این شکل نوشته میشه: (اثبات)

حالا با توجه به اینکه قطرِ مربع هایِ قضیۀ قبل، همون قطرِ نیم دایره ها هستن، از رابطه یِ دومِ قضیۀ قبل استفاده می کنیم تا نسبتِ ناحیۀ سبز رنگ به کل دایره به دست بیاد:

از اون جایی که نسبت سبز به کل 1/2 شد، نسب زرد به کل هم تقریبا[*] 1/2 میشه و این دو با هم برابر خواهند بود؛ در نتیجه نسبت نهایی و مطلوبِ سوال، 1 میشه.

جعبه متن مخفی: چرا تقریبا؟

به خاطر این دو قسمت زائد =)
زمانی میشه قسمت هایِ زرد و سبز رو دقیقا یکی گرفت که نواحی سبز رنگ، کاملا داخل دایره باشن تا با متمم گیری، مساحت ناحیه یِ دیگه و نسبت این دو به دست بیاد.
من سعی کردم راه حلی رو که جواب دقیق و بدون تقریب داره پیدا کنم، اما متاسفانه نشد :‌(

سپاس!^^

 

[صوراسرافيل]

كسى اثبات هلالين بقراط رو داره؟
يكى از دوستام لازم داره

 

[ardalaan]

میشه یکی رادیان رو واضح و آسون توضیح بده؟ تفاوتش با درجه چیه، چطوری به دست اومده و اینا ...

 

[Karenn]

میشه یکی رادیان رو واضح و آسون توضیح بده؟ تفاوتش با درجه چیه، چطوری به دست اومده و اینا ...

ببین با هر دو اندازه ی زاویه رو بیان میکنن
اما رادیان میگه اگه دایره 2π باشه سایر زوایا به درجه میتونن کسری از 2π باشه
پس با تناسب
( اگر Θ به زاویه x رادیان باشه )
Θ/360 = ×/2π
با تناسب تبدیل میشه دیگه
مثلا ۳۶۰ 2π باشه زاویه Θ چند درجه ست

 

[MahanGh]

داشتیم با استادم در مورد اثبات فرمول رادیکال مرکب حرف می زدیم که رسیدیم به اینجا

کسی نظری راه حلی صحبتی نداره

 

[Bay Harbor butcher]

خب خب خب. دوتا نقطه داریم که کمان 30 درجه تشکیل میدن. یه نقطه دیگه رندوم روی محیط دایره انتخاب میکنیم. چقدر احتمال داره که مرکز دایره توی این مثلثی باشه که توسط اون سه تا نقطه روی محیط درست شده؟

 

[Bay Harbor butcher]

خب یک سوال دیگه
مجموعِ معکوسِ شمارنده های یک عدد کامل، چند میشود؟

جعبه متن مخفی: عدد کامل چیه؟

عدد کامل یه عددیه که برابر باشه با مجموع شمارنده های کوچک تر از خودش. مثل 6. که 6=1+2+3

 

[ماهرو]

میشه بگید این سوال چند حالت داره
همه نقاطی که از دو خط متقاطعaوb به یک فاصله هستن و فاصله شون از دو نقطه xوy در همون صفحه،یکسان هست.

 

[Bay Harbor butcher]

میشه بگید این سوال چند حالت داره
همه نقاطی که از دو خط متقاطعaوb به یک فاصله هستن و فاصله شون از دو نقطه xوy در همون صفحه،یکسان هست.

خب باید تقاطع سه خط رو بررسی کنید
نقاطی که از دو خط متقاطع a و b به یک فاصله ان، روی دو خطچین عمود برهم قرار میگیرن
نقاطی که از دو نقطه xوy به یک فاصله ان، روی عمود منصف پاره خط xy قرار میگیرن
حالا جاهایی که این 3 خط چین همدیگه رو قطع میکنن، میشه نقاطی که هم از خطوط a و b به یک فاصله ان، هم از نقاط x و y
که طبق شکل سه حالت داره: 2جواب،1جواب یا بی شمار جواب

 

[ماهرو]

اثبات این رو میدونید؟
فرض:
a<b+c
b<a+c
c<a+b
حکم:
b_c|<a<b+c|

 

[امین]

اثبات این رو میدونید؟
فرض:
a<b+c
b<a+c
c<a+b
حکم:
b_c|<a<b+c|

ببین کافیه دو به دو این رابطه‌ها رو از هم کم کنی
b<a+c
c<a+b
نتیجه‌ی تفاضل این دوتا از هم این میشه
b-c<c-b
2b<2c
b<c
حالا برای دو رابطه‌ی دیگه این کارو انجام میدی
a-b<b-a
2a<2b
a<b
در کل به چنین رابطه‌ای می‌رسی که a<b<c
پس بدیهیه وقتی a از b کوچیک‌تره و خود b هم از c کوچیک‌تره پس a از مجموع b و c هم کوچیک‌تر میشه؛ پس یعنی یک سمت حکم ثابت شد a<b+c
از طرفی ما بنا به فرض داشتیم c<a+b و این یعنی اگه b رو به اون سمت ببریم میشه c-b<a و چون b از c کوچیک‌تره، می‌تونیم به طور کلی اعلام کنیم b-c هم کوچیک‌تر از a عه، و این یعنی قدرمطلق تفاضل b و c در هر حالتی از a کوچیک‌تره و طرف دیگه‌ی حکم هم به اثبات می‌رسه.

 

[Bay Harbor butcher]

یک چهار ضلعی محدب با قطر های 6و7 داریم.
محیط چهار ضلعی کدام میتواند باشد؟
1) 15
2)10
3)27

 

[Bay Harbor butcher]

1

خو چرا؟

 

[Bay Harbor butcher]

2؟

اینم اثبات کنی ممنونت میشم
بعد کلاست

 

[Bay Harbor butcher]

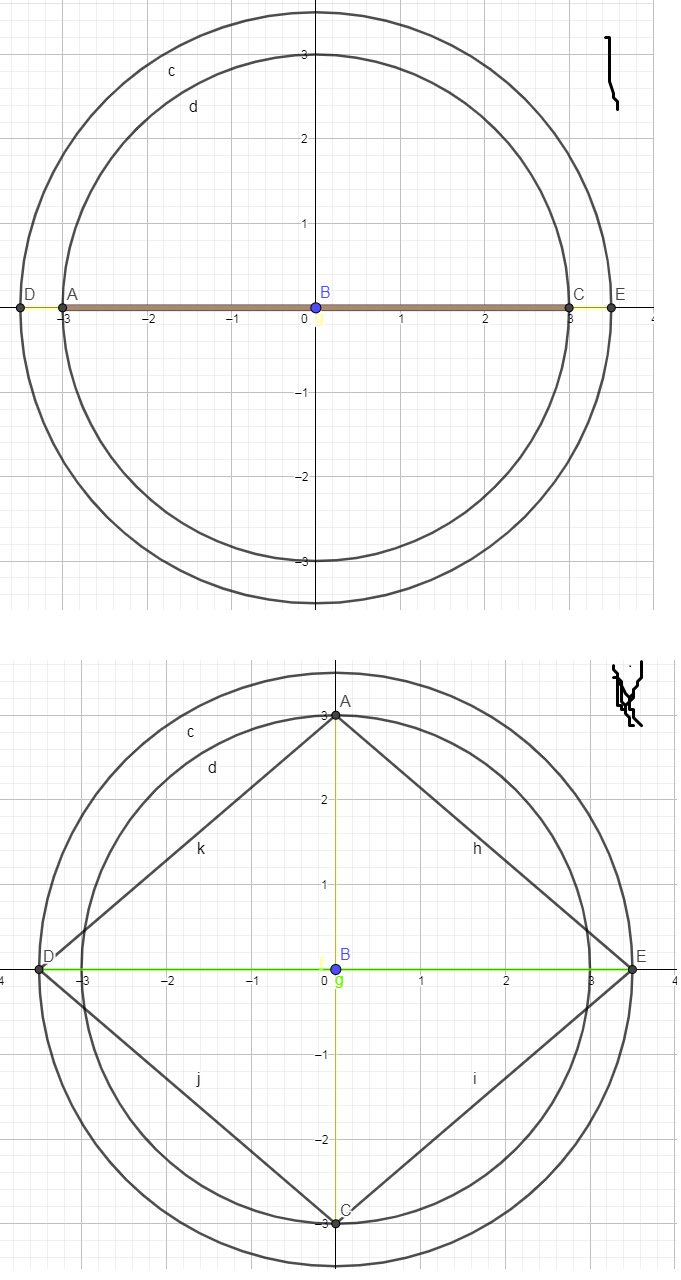
تو حالت 1 که دو تا قطر روی هم افتادن و زاویه بینشون صفره هیچ اتفاق خاصی نمیوفته اما اگه یکمی زاویه بیشتر بشه چهار ضلعی تشکیل میشه و حساب کردن محیطش دردسره پس برای حالت 1 مجموع دو قطر یا همون 13 رو در نظر میگیریم


تو حالت دوم هم که حداکثر زاویه رو دارن محیطش تقریبا میشه 18.04 (طول یک ضلع * چهار که با فیثاقورث درمیاد)

پس محیط میتونه بین اینا باشه
13<x< هیجده


حالا جواب درسته یا دارم چرت و پرت میبافم؟

شک م هم این بود که اگه منصف هم نباشن چی و دیدم حالت های زیادی هست

ببین فکر کنم که راه حلت خییلی درست نیست. به همون دلیلی که تو خط اخر گفتی
من این شکلی رفتم که مطمئن تره(اون نامساوی ها از اصل حمار استفاده شده) :

 

[./.]

اینم اثبات کنی ممنونت میشم
بعد کلاست

حاصل جمع مطلوب عبارتست از جمع مجموعه کسرهایی که صورتشان 1 و مخرجشان شمارنده های آن عدد از جمله خود آن عدد اند. پس مخرج مشترک را خود آن عدد میگیریم و صورت ها هرکدام باید در حاصل تقسیم آن عدد بر خود -که عبارتست از شمارندۀ دیگری از آن عدد- ضرب شوند و از آنجا که صورت ها یک اند، پس صورت کسر حاصل عبارت خواهد شد از تمام شمارنده های آن عدد. -زیرا هر شمارنده از تقسیم آن عدد بر شمارندۀ متناظر به دست می اید. مثلا در مثال 6، 2 از تقیم 6 بر 3 پیش می اید و 3 برعکس- حال چون عدد کامل است، مجموع شمارنده های کوچکتر از خودش برابر با خودش خواهند شد و خودش هم که در صورت حضور دارد، پس دو برابر خود عدد در صورت است و خودش هم که در مخرج بود، پس حاصل 2 خواهد شد.

 

[Lushato]

در برابر سوالای شما که چیزی نیست
ولی خب نمیدونم چیکارش کنم....

 

[Bay Harbor butcher]

در برابر سوالای شما که چیزی نیست
ولی خب نمیدونم چیکارش کنم....

مساحت مربع که x^2 هست
مساحت دایره هم p*r^2
حالا برای مساحت دایره به جای r، مقداری که بر حسب ایکس داده رو جای گذاری میکنی
تهش این دوتا رو باهم جمع میکنی
یه عبارتی بهت میده بر حسب x که عبارته مساویه 6 هست
که بعد میتونی از اون x رو بدست بیارید
اگه بازم سوال داشتید بگید که عکس بگیرم بفرستم

در برابر سوالای شما که چیزی نیست
ولی خب نمیدونم چیکارش کنم....

?

 

[Bay Harbor butcher]

?

حالا یه مرحله جلوتر:

?
پ ن: ترجیحا دانشگاهی ها حل نکنن، بزارن برای دبیرستانی ها یه چالشی بشه!