پاسخ : سوالات ریاضی
خوب، نمی دونم این به جایی می رسه یا نه، ولی دیگه فکرم بیشتر از این کفاف نمی ده...!
اول از همه در نظر داشته باشیم که معادله بیضی می شه 1. x^2 + (ky)^2 = r^2، البته وقتی قطراش روی محور مختصاته یعنی قبل از چرخوندنش).
حالا می خوایم معادله بیضی جدید رو، بعد از چرخوندن به دست بیاریم. هر نقطه ای که روی بیضی اول در نظر بگیریم، بعد از چرخش هم با مختصات جدیدش روی بیضی جدید هم هست، ولی با مختصات جدید 'x و 'y. از اونجایی که معادله ی اول بر حسب x و y هست، لازمه این 'x و 'y رو هم بر حسب یه عباراتی از x و y بنویسیم.
اول 'x و

یه نقطه در نظر میگیریم روی بیضی اول، به فاصله ی s از مرکز مختصات، و به زاویه b از محور x. قبل از چرخش بیضی، مولفه x نقطه هه میشه x = s.cos(b) .2. بعد از چرخش با زاویه a، زاویه ی همون نقطه از محور عوض می شه و می شه a+b، پس مولفه 'x نقطه هه میشه x' = s.cos(a+b) .3. در واقع، با استفاده از نسبت این دو تا، می تونیم بنویسیم x' = x.(cos(a+b)/cos(b)) .4. بعد صورت این عبارت کسینوسی رو با استفاده از همون اتحاد مثلثاتیه باز می کنیم، می شه x' = x.(cos(a)cos(b)-sin(a)sin(b)/cosb) .5 .
از این جا به بعدش دیگه داغون می شه، در حدی که باعث می شه به این نتیجه برسم که راه حل درست این نیست! اینجوریه که می خوایم عبارت 5 رو ساده تر کنیم و مجهولا رو از بین ببرین. cosb و sinb به ترتیب می شن x/s و y/s. با فیثاغورث هم که s میشه رادیکال x^2 + y^2 . پس cosb و sinb رو می تونیم بر حسب فقط x و y بنویسیم. ولی هنوز این هم کافی نیست، چون تو رابطه مون برای x و 'x نمی خوایم y داشته باشیم. پس با استفاده از رابطه ی 1 برای بیضی، y رو هم بر حسب x می نویسیم! نتیجه می شه که cosb و sinb فقط بر حسب x نوشته می شن، و اونا رو می ذاریم سر جاشون تو عبارت 5. کل عباری می شه 'x بر حسب یه عبارت خیلی زشت از x!
یه کم نفس نفس می زنیم، یه نفس عمیق می کشیم، بعد همین کار رو برای y و 'y هم تکرار می کنیم! بعد یه کم گریه می کنیم و ادامه می دیم...!
حالا در واقع عبارتی رو که مولفه هر نقطه روی بیضی دوم رو بر حسب مولفه های همون نقطه قبل از چرخش به دست آوردیم. حالا این به چه دردی می خوره؟! خوب شاید بشه ازش استفاده کرد برای این که معادله بیضی دوم رو بنویسیم. اینطوری که عبارات به دست اومده رو یه کم جابجا می کنیم و اینا، طوری که x بر حسب 'x و y بر حسب 'y باشه به جای برعکسش... بعدش این دو تا عبارت آخری رو جاگذاری میکنیم توی همون رابطه 1 که معادله بیضی جدید به دست بیاد... (

! )
حالا که معادله بیضی رو بعد از چرخش داریم، بقیه ش نسبتا آسونه. دو تا معادله دیگه هم داریم، که معادله خطهای عمودیه که رسم می کنیم. برای اون خطها هم شیب رو که می دونیم، چون قطر اصلی بعد از چرخش معادله ش می شه y' = tan(a). x' .6 ، پس شیب خط عمود بهش می شه وارون و منفی tana. مختصات C و D رو هم که داریم، پس معادله اون دو تا خط عمود رو راحت با استفاده از اون شیب و مختصات این دو تا می نویسیم. ('x و 'y استفاده کردم، چون مختصاتمون برای بیضی جدیده).
معادله هر کدوم از اون خطها رو با معادله بیضی مساوی قرار می دیم و حل می کنیم، مختصات نقطه تقاطع باید بشه جوابشون، که ما داریم اون مختصات رو. پس دو تا دستگاه داریم، که جواب هر دو تا دستگاه رو می دونیم، ولی صورت معادله هاش بر حسب یه سری مجهوله. پس با حل کردن دو تا دستگاه، که توش معادله هاش a و k مجهولن، ولی 'x و 'y متعلق به جوابای معادله ها رو داریم، احتمالا به یه جوابی می رسیم دیگه...!
(ایشالا...!

)
پ.ن. شاید یه خورده گمراه کننده باشه و اینا... احتمالا راه حل خیلی ساده تری داره که من بلد نیستم... اینم شاید اصلا جواب نده حتی :)





















 :-[
:-[


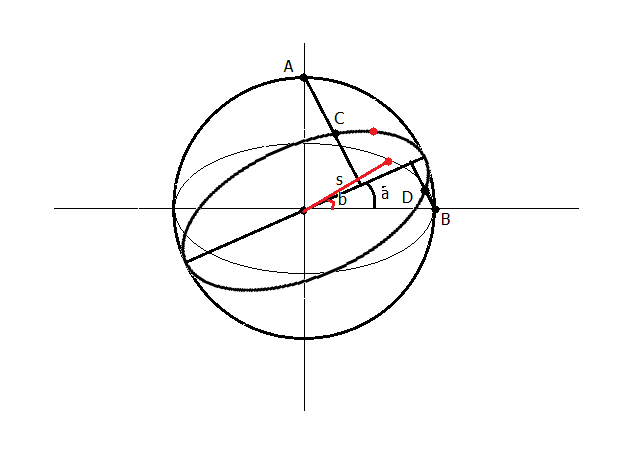
 یه نقطه در نظر میگیریم روی بیضی اول، به فاصله ی s از مرکز مختصات، و به زاویه b از محور x. قبل از چرخش بیضی، مولفه x نقطه هه میشه x = s.cos(b) .2. بعد از چرخش با زاویه a، زاویه ی همون نقطه از محور عوض می شه و می شه a+b، پس مولفه 'x نقطه هه میشه x' = s.cos(a+b) .3. در واقع، با استفاده از نسبت این دو تا، می تونیم بنویسیم x' = x.(cos(a+b)/cos(b)) .4. بعد صورت این عبارت کسینوسی رو با استفاده از همون اتحاد مثلثاتیه باز می کنیم، می شه x' = x.(cos(a)cos(b)-sin(a)sin(b)/cosb) .5 .
یه نقطه در نظر میگیریم روی بیضی اول، به فاصله ی s از مرکز مختصات، و به زاویه b از محور x. قبل از چرخش بیضی، مولفه x نقطه هه میشه x = s.cos(b) .2. بعد از چرخش با زاویه a، زاویه ی همون نقطه از محور عوض می شه و می شه a+b، پس مولفه 'x نقطه هه میشه x' = s.cos(a+b) .3. در واقع، با استفاده از نسبت این دو تا، می تونیم بنویسیم x' = x.(cos(a+b)/cos(b)) .4. بعد صورت این عبارت کسینوسی رو با استفاده از همون اتحاد مثلثاتیه باز می کنیم، می شه x' = x.(cos(a)cos(b)-sin(a)sin(b)/cosb) .5 .  ! )
! )