You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
aliila
کاربر نیمهفعال

- ارسالها
- 13
- امتیاز
- 7
- نام مرکز سمپاد
- امام حسن مجتبی
پاسخ : سوالات ریاضی
به نظر من این دوکمیت بی نهایت هتدسی است ومی توان ازطریق مشاهده مقایسه راانجام داد.باتوجه به تعریف خط (خط امتداد نقطه است.
بر اثر حرکت و امتداد یک نقطه بر صفحه در یک راستا خط شکل می گیرد.)،تعدادنقاط باطول خط متناسب است.منظور نیلوفر رانفهمیدم.
به نقل از سیاوش :میشه این نکته رو توضیح بدین ؟
هر کمان یا پاره خط هر قدر هم که کوچیک باشه میگیم از بینهایت نقطه تشکیل شده . چه طوری 2 کمیت بی نهایت رو مقایسه میکنیم ؟
به نظر من این دوکمیت بی نهایت هتدسی است ومی توان ازطریق مشاهده مقایسه راانجام داد.باتوجه به تعریف خط (خط امتداد نقطه است.
بر اثر حرکت و امتداد یک نقطه بر صفحه در یک راستا خط شکل می گیرد.)،تعدادنقاط باطول خط متناسب است.منظور نیلوفر رانفهمیدم.
- ارسالها
- 1,667
- امتیاز
- 6,103
- نام مرکز سمپاد
- شهید بهشتی
- شهر
- شهرکرد
- سال فارغ التحصیلی
- 92
- دانشگاه
- صنعتی شریف
- رشته دانشگاه
- مهندسی کامپیوتر- نرم افزار
پاسخ : سوالات ریاضی

توی اثبات هیچ وقت از شهود استفاده نمیکنیم .به نقل از aliila :به نظر من این دوکمیت بی نهایت هتدسی است ومی توان ازطریق مشاهده مقایسه راانجام داد.باتوجه به تعریف خط (خط امتداد نقطه است.
بر اثر حرکت و امتداد یک نقطه بر صفحه در یک راستا خط شکل می گیرد.)،تعدادنقاط باطول خط متناسب است.منظور نیلوفر رانفهمیدم.

Niloofar sharafi
کاربر فوقحرفهای

- ارسالها
- 1,159
- امتیاز
- 2,807
- نام مرکز سمپاد
- فرزانگان 1 تهران
- شهر
- تهران
- مدال المپیاد
- -
- دانشگاه
- شریف
- رشته دانشگاه
- ریاضیات و کاربرد ها
پاسخ : سوالات ریاضی
خب اینی که داری سعی می کنی اثباتش کنی ، یکی از اصول هندسه اقلیدسیه !
بدون داشتن این اصل ، اصلا نمی تونی بگی پاره خط AB رو رسم می کنیم و امتداد می دیم تا فلان چیزو تو فلان جا قطع کنه ! چون اصلا معلوم نیست چنین پاره خطی وجود داشته باشه ! یا مثلا دو تا از این پاره خطا نداشته باشیم !
بله بله ! غلط است !
کلا هم این اثبات می شه که تعداد نقاط روی دو تا خط با طول متفاوت برابرند . اثباتش مشابه همین اثباته که میگن بازه [0,1] از اعداد حقیقی ، به اندازه کل اعداد حقیقی توش عدد وجود داره !
این جوری اثبات می شه که تو میای این دو تا کمانو تغییر شکل می دی تا به دو تا خط تبدیل بشه . طولشون متفاوته دیگه حالا دو سر این خطوط رو متناظرا به هم وصل می کنی و ادامه می دی تا همو قطع کنن .
در نهایت یه مثلث بوجود میاد که یه خط وسطشه . قاعده مثلث و اون خطه هم که همون خط هایی که خودت رسم کردی .
بعد هر نقطه از قاعده مثلث یا اون خط رو در نظر بگیری ، می تونی یه نقطه متناظر پیدا کنی تو اون یکی . این جوری که میای نقطه مورد نظرت رو به راس مثلث وصل می کنی ، بعد ادامه می دی تا اون یکی رو قطع کنه .
این جوری با تناظر یک به یک ثابت می شه که تعداد نقاط این دو خط برابره .
یکی دو بار نوشته مو بخون ، اگه متوجه نشدی بگو شکل بکشم برات .
* کلا هم تو ریاضیات ، با روش های مشابه یا غیر مشابه این ، چیز های ثابت می شه که شاید به نظرت عجیب بیاد .
مثلا اینکه تعداد اعداد گویا با اعداد طبیعی برابره !
یا اینکه تعداد اعداد زوج با کل اعداد طبیعی برابره .
یا هر دنباله حسابی یا هندسی روی اعداد طبیعی که کراندار نباشه ، تعداد اعضاش به اندازه تعداد اعضای کل اعداد طبیعیه !
و ...
اینا یه بحثای جالبیه که درباره "بی نهایت " دنبال می کنن . البته اینا مثال های ساده ای از اوناس . خواستی می تونی مطالعه کنی در موردشون .
به نقل از aliila :به نظر من این دوکمیت بی نهایت هتدسی است ومی توان ازطریق مشاهده مقایسه راانجام داد.باتوجه به تعریف خط (خط امتداد نقطه است.
بر اثر حرکت و امتداد یک نقطه بر صفحه در یک راستا خط شکل می گیرد.)،تعدادنقاط باطول خط متناسب است.منظور نیلوفر رانفهمیدم.
خب اینی که داری سعی می کنی اثباتش کنی ، یکی از اصول هندسه اقلیدسیه !
بدون داشتن این اصل ، اصلا نمی تونی بگی پاره خط AB رو رسم می کنیم و امتداد می دیم تا فلان چیزو تو فلان جا قطع کنه ! چون اصلا معلوم نیست چنین پاره خطی وجود داشته باشه ! یا مثلا دو تا از این پاره خطا نداشته باشیم !
به نقل از aliila :یهنی اینکه (تعداد نقاط با طول متناسب است) غلط است؟
بله بله ! غلط است !
کلا هم این اثبات می شه که تعداد نقاط روی دو تا خط با طول متفاوت برابرند . اثباتش مشابه همین اثباته که میگن بازه [0,1] از اعداد حقیقی ، به اندازه کل اعداد حقیقی توش عدد وجود داره !
این جوری اثبات می شه که تو میای این دو تا کمانو تغییر شکل می دی تا به دو تا خط تبدیل بشه . طولشون متفاوته دیگه حالا دو سر این خطوط رو متناظرا به هم وصل می کنی و ادامه می دی تا همو قطع کنن .
در نهایت یه مثلث بوجود میاد که یه خط وسطشه . قاعده مثلث و اون خطه هم که همون خط هایی که خودت رسم کردی .
بعد هر نقطه از قاعده مثلث یا اون خط رو در نظر بگیری ، می تونی یه نقطه متناظر پیدا کنی تو اون یکی . این جوری که میای نقطه مورد نظرت رو به راس مثلث وصل می کنی ، بعد ادامه می دی تا اون یکی رو قطع کنه .
این جوری با تناظر یک به یک ثابت می شه که تعداد نقاط این دو خط برابره .
یکی دو بار نوشته مو بخون ، اگه متوجه نشدی بگو شکل بکشم برات .
* کلا هم تو ریاضیات ، با روش های مشابه یا غیر مشابه این ، چیز های ثابت می شه که شاید به نظرت عجیب بیاد .
مثلا اینکه تعداد اعداد گویا با اعداد طبیعی برابره !
یا اینکه تعداد اعداد زوج با کل اعداد طبیعی برابره .
یا هر دنباله حسابی یا هندسی روی اعداد طبیعی که کراندار نباشه ، تعداد اعضاش به اندازه تعداد اعضای کل اعداد طبیعیه !
و ...
اینا یه بحثای جالبیه که درباره "بی نهایت " دنبال می کنن . البته اینا مثال های ساده ای از اوناس . خواستی می تونی مطالعه کنی در موردشون .
- ارسالها
- 1,667
- امتیاز
- 6,103
- نام مرکز سمپاد
- شهید بهشتی
- شهر
- شهرکرد
- سال فارغ التحصیلی
- 92
- دانشگاه
- صنعتی شریف
- رشته دانشگاه
- مهندسی کامپیوتر- نرم افزار
پاسخ : سوالات ریاضی
بحث درباره ی بینهایت شد من قبلا یه مقاله در باره ی بینهایت خونده بودم که خیلی به درک بینهایت کمک میکنه .
این مقاله توسط ديويد هيلبرت، رياضيدان بزرگ آلماني براي درك راحتتر بينهايت مطرح شده و توسط آقاي محمد صالح زارعپور بازنويسي شده.
از اینجا میتونید دانلودش کنید .
پیش نهاد میکنم حتما حتما حتما بخویندش هم خیلی سرگرم کنندست هم جالب هم آموزنده .
بحث درباره ی بینهایت شد من قبلا یه مقاله در باره ی بینهایت خونده بودم که خیلی به درک بینهایت کمک میکنه .
این مقاله توسط ديويد هيلبرت، رياضيدان بزرگ آلماني براي درك راحتتر بينهايت مطرح شده و توسط آقاي محمد صالح زارعپور بازنويسي شده.
از اینجا میتونید دانلودش کنید .
پیش نهاد میکنم حتما حتما حتما بخویندش هم خیلی سرگرم کنندست هم جالب هم آموزنده .
amin.14
کاربر فوقفعال

- ارسالها
- 92
- امتیاز
- 77
- نام مرکز سمپاد
- دبیرستان علامه حلی
- شهر
- تهران
- دانشگاه
- هر جا خدا بخواهد!
پاسخ : سوالات ریاضی
سلام به همگی.
من در تعریف ضرب و توان دچار شبهه شدم.دوستان لطفا رفع ابهام کنند.
مسلما تعریف ضرب در ریاضی،a بار جمع کردن b با خودش نیست.چون a لزوما طبیعی نیست.
همین طور برای توان.تعریف ما باید در مورد
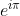 هم نظر بده.
هم نظر بده. 
مرسی از همگی
سلام به همگی.
من در تعریف ضرب و توان دچار شبهه شدم.دوستان لطفا رفع ابهام کنند.

مسلما تعریف ضرب در ریاضی،a بار جمع کردن b با خودش نیست.چون a لزوما طبیعی نیست.

همین طور برای توان.تعریف ما باید در مورد

مرسی از همگی

Ali Monsefi
کاربر فعال

- ارسالها
- 73
- امتیاز
- 111
- نام مرکز سمپاد
- وات؟
- شهر
- تهران
- مدال المپیاد
- مدال نقرهی المپیاد ریاضی کشوری ۹۲
پاسخ : سوالات ریاضی
البته داویت هیلبرت فقط تو یه سخنرانیش در حد چند جمله مثال هتل رو زده و بعداً بقیه، هتل هیلبرتو سوژه کردن!به نقل از سیاوش :بحث درباره ی بینهایت شد من قبلا یه مقاله در باره ی بینهایت خونده بودم که خیلی به درک بینهایت کمک میکنه .
این مقاله توسط ديويد هيلبرت، رياضيدان بزرگ آلماني براي درك راحتتر بينهايت مطرح شده و توسط آقاي محمد صالح زارعپور بازنويسي شده.
از اینجا میتونید دانلودش کنید .
پیش نهاد میکنم حتما حتما حتما بخویندش هم خیلی سرگرم کنندست هم جالب هم آموزنده .
- ارسالها
- 3,112
- امتیاز
- 12,764
- نام مرکز سمپاد
- .
- شهر
- .
- سال فارغ التحصیلی
- 1392
- مدال المپیاد
- فیزیک
- دانشگاه
- شریف
- رشته دانشگاه
- فیزیک
پاسخ : سوالات ریاضی
مجموعه ی رئوس a1 تا an داریم .
چند گراف دو منتظم میشه با این مجموعه رأس ها تشکیل داد ؟
راه ساده ی شمارشی داره ؟
مجموعه ی رئوس a1 تا an داریم .
چند گراف دو منتظم میشه با این مجموعه رأس ها تشکیل داد ؟
راه ساده ی شمارشی داره ؟
Niloofar sharafi
کاربر فوقحرفهای

- ارسالها
- 1,159
- امتیاز
- 2,807
- نام مرکز سمپاد
- فرزانگان 1 تهران
- شهر
- تهران
- مدال المپیاد
- -
- دانشگاه
- شریف
- رشته دانشگاه
- ریاضیات و کاربرد ها
پاسخ : سوالات ریاضی
خیلی بستگی به n داره
کلللی توضیحش طولانی میشه
فقط در همین حد بگم که باید به یک یا چند مولفه تقسیمش کرد که تو هر کدوم ، راسا رو پشت سر هم به وصل می کنیم ، دایره وار مثلا ! ( اگه لازمه بگید شکل بکشم . ) ( میشه مثلا :a1 , a2 , a3, ... ak , a1 )
بعد پس هر کدوم از این مولفه ها ، باید لااقل 3 تا راس داشته باشن دیگه .
حالا واسه همین می گم جواب سوال خیلی ربط داره به n .
به نقل از H O S E I N :مجموعه ی رئوس a1 تا an داریم .
چند گراف دو منتظم میشه با این مجموعه رأس ها تشکیل داد ؟
راه ساده ی شمارشی داره ؟
خیلی بستگی به n داره
کلللی توضیحش طولانی میشه
فقط در همین حد بگم که باید به یک یا چند مولفه تقسیمش کرد که تو هر کدوم ، راسا رو پشت سر هم به وصل می کنیم ، دایره وار مثلا ! ( اگه لازمه بگید شکل بکشم . ) ( میشه مثلا :a1 , a2 , a3, ... ak , a1 )
بعد پس هر کدوم از این مولفه ها ، باید لااقل 3 تا راس داشته باشن دیگه .
حالا واسه همین می گم جواب سوال خیلی ربط داره به n .
- ارسالها
- 3,112
- امتیاز
- 12,764
- نام مرکز سمپاد
- .
- شهر
- .
- سال فارغ التحصیلی
- 1392
- مدال المپیاد
- فیزیک
- دانشگاه
- شریف
- رشته دانشگاه
- فیزیک
پاسخ : سوالات ریاضی
میخواستم این سوالو حل کنم گفتم شاید با گراف بشه . حالا که دردسر داره خود سواله رو بگین چجوری حل میشه لطفا :
ده نفر داریم که هر کدوم یه کلاه دارن . همه کلاهشون رو میندازن توی یه جعبه . بعد با هم به صورت تصادفی هر کدوم یه کلاه برمیدارن . احتمال این که حداقل یک نفر کلاه خودشو برداره چقدره .
قسمت دومش : حالا فرض کنید نوبتی کلاه بردارن از تو جعبه .
میخواستم این سوالو حل کنم گفتم شاید با گراف بشه . حالا که دردسر داره خود سواله رو بگین چجوری حل میشه لطفا :
ده نفر داریم که هر کدوم یه کلاه دارن . همه کلاهشون رو میندازن توی یه جعبه . بعد با هم به صورت تصادفی هر کدوم یه کلاه برمیدارن . احتمال این که حداقل یک نفر کلاه خودشو برداره چقدره .
قسمت دومش : حالا فرض کنید نوبتی کلاه بردارن از تو جعبه .
مهدی
کاربر فوقحرفهای

- ارسالها
- 1,112
- امتیاز
- 7,384
- نام مرکز سمپاد
- علامهحلی
- شهر
- تهران
- مدال المپیاد
- کامپیوتر
- دانشگاه
- دانشگاه تهران. :دی
- رشته دانشگاه
- آمار. :دی
پاسخ : سوالات ریاضی
حداقل یه نفر کلاه خودشو برمیداره و حداکثر 8(چرا?!)
بعد بین اینکه هرکسی اشتباهی کلاه چه کسی رو برداره فرق هست.
بنابراین جواب برابر هست با :1تقسیم بر

قسمت دوم:
همون قسمت الف فقط یه چیزی که اضافه میشه اینه که کدوم نفرات کلاه خودشون رو بردارن یا برندارن(فرقی نداره)که میشه دوباره سیگما انتخاب iاز 10
یعنی قسمت الف انتخاب iاز10میشه به توان 2.
قسمت اول:به نقل از H O S E I N :ده نفر داریم که هر کدوم یه کلاه دارن . همه کلاهشون رو میندازن توی یه جعبه . بعد با هم به صورت تصادفی هر کدوم یه کلاه برمیدارن . احتمال این که حداقل یک نفر کلاه خودشو برداره چقدره .
قسمت دومش : حالا فرض کنید نوبتی کلاه بردارن از تو جعبه .
حداقل یه نفر کلاه خودشو برمیداره و حداکثر 8(چرا?!)
بعد بین اینکه هرکسی اشتباهی کلاه چه کسی رو برداره فرق هست.
بنابراین جواب برابر هست با :1تقسیم بر

قسمت دوم:
همون قسمت الف فقط یه چیزی که اضافه میشه اینه که کدوم نفرات کلاه خودشون رو بردارن یا برندارن(فرقی نداره)که میشه دوباره سیگما انتخاب iاز 10
یعنی قسمت الف انتخاب iاز10میشه به توان 2.
- ارسالها
- 1,667
- امتیاز
- 6,103
- نام مرکز سمپاد
- شهید بهشتی
- شهر
- شهرکرد
- سال فارغ التحصیلی
- 92
- دانشگاه
- صنعتی شریف
- رشته دانشگاه
- مهندسی کامپیوتر- نرم افزار
پاسخ : سوالات ریاضی
آقا ورد نداری توی اینجا بنویس :
www.codecogs.com/latex/eqneditor.php
من الان اصلا نفهمیدم چی گفتی
به نقل از مَِهدی.ش :قسمت اول:
حداقل یه نفر کلاه خودشو برمیداره و حداکثر 8(چرا?!)
بعد بین اینکه هرکسی اشتباهی کلاه چه کسی رو برداره فرق هست.
بنابراین جواب برابر هست با :1تقسیم بر سیگما i=1تا 8 (i-1)!*انتخاب iاز10
(ببخشید دیگه الان با دسترسی به ورد ندارم)
قسمت دوم:
همون قسمت الف فقط یه چیزی که اضافه میشه اینه که کدوم نفرات کلاه خودشون رو بردارن یا برندارن(فرقی نداره)که میشه دوباره سیگما انتخاب iاز 10
یعنی قسمت الف انتخاب iاز10میشه به توان 2.
آقا ورد نداری توی اینجا بنویس :
www.codecogs.com/latex/eqneditor.php
من الان اصلا نفهمیدم چی گفتی
- ارسالها
- 1,667
- امتیاز
- 6,103
- نام مرکز سمپاد
- شهید بهشتی
- شهر
- شهرکرد
- سال فارغ التحصیلی
- 92
- دانشگاه
- صنعتی شریف
- رشته دانشگاه
- مهندسی کامپیوتر- نرم افزار
پاسخ : سوالات ریاضی
من فکر کنم راه حلت اشتباه باشه .
فرض کنیم 3 نفر باشن . احتمال به دست اومده میشه 4/6 =2/3 اما با اون رابطه ای که شما نوشتی میشه 1/3
این سواله با اصل شمول عدم شمول حل میشه ولی خیلی طولانیه و حوصله میخواد
به نقل از مَِهدی.ش :قسمت اول:
حداقل یه نفر کلاه خودشو برمیداره و حداکثر 8(چرا?!)
بعد بین اینکه هرکسی اشتباهی کلاه چه کسی رو برداره فرق هست.
بنابراین جواب برابر هست با :1تقسیم بر

قسمت دوم:
همون قسمت الف فقط یه چیزی که اضافه میشه اینه که کدوم نفرات کلاه خودشون رو بردارن یا برندارن(فرقی نداره)که میشه دوباره سیگما انتخاب iاز 10
یعنی قسمت الف انتخاب iاز10میشه به توان 2.
من فکر کنم راه حلت اشتباه باشه .
فرض کنیم 3 نفر باشن . احتمال به دست اومده میشه 4/6 =2/3 اما با اون رابطه ای که شما نوشتی میشه 1/3
این سواله با اصل شمول عدم شمول حل میشه ولی خیلی طولانیه و حوصله میخواد

F@temeh
کاربر خاکانجمنخورده

- ارسالها
- 1,877
- امتیاز
- 15,504
- نام مرکز سمپاد
- فرزانگـــان
- شهر
- کاشـــان
- مدال المپیاد
- مرحله اول ریاضی
- دانشگاه
- پلی تکنیک
- رشته دانشگاه
- سخت افزار
پاسخ : سوالات ریاضی
اینکه باهم بردارن کلاه هارو یا نوبتی فرقی داره؟ ینی تعدادش فرق نمیکنه که
ینی مثلا اینکه کی کلاه خودشُ برداره یا برنداره تو هردوتا قسمت سوال هست. پس تعدادش فرقی نداره.
داره؟

اینکه باهم بردارن کلاه هارو یا نوبتی فرقی داره؟ ینی تعدادش فرق نمیکنه که

به نقل از مَِهدی.ش :قسمت دوم:
همون قسمت الف فقط یه چیزی که اضافه میشه اینه که کدوم نفرات کلاه خودشون رو بردارن یا برندارن(فرقی نداره)که میشه دوباره سیگما انتخاب iاز 10
یعنی قسمت الف انتخاب iاز10میشه به توان 2.
ینی مثلا اینکه کی کلاه خودشُ برداره یا برنداره تو هردوتا قسمت سوال هست. پس تعدادش فرقی نداره.
داره؟


Niloofar sharafi
کاربر فوقحرفهای

- ارسالها
- 1,159
- امتیاز
- 2,807
- نام مرکز سمپاد
- فرزانگان 1 تهران
- شهر
- تهران
- مدال المپیاد
- -
- دانشگاه
- شریف
- رشته دانشگاه
- ریاضیات و کاربرد ها
پاسخ : سوالات ریاضی
راه حل قسمت اول یه ایرادی داره . اونم اینه که توی اون فاکتوریله ، یه سریا ممکنه با خودشون متناظر بشن . بعد کلی حالت تکراری پیدا می کنه .
علاوه بر این فک کنم اونی که نوشتید ، باید حداکثر 9 تا باشه .
راه حلی که من برا این سوال دارم ، از یه مفهومی به عنوان پریش استفاده می کنه .
حالا پریش چیه ؟
با یه مثال توضیح می دم .
مثلا تو همین سوال ، اگه بیایم این 10 تا کلاهو ، طوری بین این نفر تقسیم کنیم ، که مطمئن باشیم به هیچ کس ، کلاه خودش نمی رسه ، ما یه پریش 10 تایی ساختیم .
فهمیدید پریش چیه ؟
پس ما اول باید یه راهی ارائه بدیم که تعداد پریش های n تایی رو اول محاسبه کنیم واسه این سوال .
یه راهی برای این محاسبه وجود داره ، که با استفاده از عدد e یا همون عدد نپر هستش . ( تو اینترنت ، هم می تونید در مورد e بیشتر مطالعه کنید ، هم شاید بتونید این فرمول رو بدست بیارید . )
اما یه راه استقرایی هم داره محاسبه این عدد . فرض کنید که ما ، تعداد پریش های 1 تا k تایی رو محاسبه کردیم . ( من راستش خودم علامتی که به عنوان "تعداد پریش های n تایی استفاده میشه رو بلد نیستم ! به اختصار می نویسم :"تپ(k)" ) حالا برای محاسبه تپ(k+1) ، از مکمل گیری استفاده می کنیم .
به این صورت که می گیم همه حالت های برداشتن این کلاه ها (یعنی (k+1)! ) منهای حالت هایی حداقل یه نفر کلا خودشو بر می داره .
مشابه روشی که آقای مهدی اون بالا گفتن ، میایم حالت بندی می کنیم رو تعداد کسایی که کلاه خودشونو بر می دارن . منتهی به جای اینکه اون انتخابه رو تو اون فاکتوریله ضرب کنیم ، تو تپ(k+1-i) ضرب می کنیم . پس ما الآن تپ (i+1) رو هم محاسبه کردیم به استقرا .
حالا پس جواب سوال ، میشه همونی که آقای مهدی نوشتن ، فقط به جای اون فاکتوریله ، باید تپ(10-i ) تو اون انتخاب ضرب شه .
البته این کل حالت هاست . پس احتمال کل ، میشه این عددی که بالا محاسبه کردیم ، تقسیم بر 10! .
یا در واقع ، جواب میشه 1 منهای حاصل تقسیم تپ(10) بر 10! .
اما برای قسمت دوم ، ایده من اینه که از قبلیه استفاده کنیم .
برای محاسبه کل حالت ها ، به نظر من به جای 10! حالت ، 10! × 10! حالت داریم . یعنی به 10! حالت ، میایم نوبت ها رو به آدما نسبت می دیم ، و به 10! حالت ، میایم آدما رو به کلاها نسبت می دیم .
برای محاسبه حالت های نامطلوب هم ، باید همه رو تو یه صف بچینیم ( یعنی به هر کسی نوبتی نسبت بدیم که 10! حالت داره ) و بعد یه پریش 10 تایی درست کنیم .
پس بازم جواب سوال ، می شه 1 منهای حاصل تقسیم 10! × تپ (10) بر !10×10! . یعنی احتمالش با بالایی یکیه !
برا اینکه یه کم شهود پیدا کنید ، که چرا این دو تا احتمال برابر شدن ، فک کنید که اگه مثلا تو حالت اول ، یه نفر با کلاهی که بهش نسبت می دیم رو حذف کنیم ، شرایطی که ایجاد میشه ، مثل حالتیه که وقتی تو قسمت دوم ، نفر اول کلاهشو برمیداره ، ایجاد میشه . در واقع ، ترتیب وایسادن اینا ، تو کلاهی که بهشون نسبت می دیم ، تاثیری نداره . چون هر کسیو و کلاهش ، مستقل از بقیه ن .
خیلی پیچیده شد
به نقل از H O S E I N :میخواستم این سوالو حل کنم گفتم شاید با گراف بشه . حالا که دردسر داره خود سواله رو بگین چجوری حل میشه لطفا :
ده نفر داریم که هر کدوم یه کلاه دارن . همه کلاهشون رو میندازن توی یه جعبه . بعد با هم به صورت تصادفی هر کدوم یه کلاه برمیدارن . احتمال این که حداقل یک نفر کلاه خودشو برداره چقدره .
قسمت دومش : حالا فرض کنید نوبتی کلاه بردارن از تو جعبه .
به نقل از مَِهدی.ش :قسمت اول:
حداقل یه نفر کلاه خودشو برمیداره و حداکثر 8(چرا?!)
بعد بین اینکه هرکسی اشتباهی کلاه چه کسی رو برداره فرق هست.
بنابراین جواب برابر هست با :1تقسیم بر

قسمت دوم:
همون قسمت الف فقط یه چیزی که اضافه میشه اینه که کدوم نفرات کلاه خودشون رو بردارن یا برندارن(فرقی نداره)که میشه دوباره سیگما انتخاب iاز 10
یعنی قسمت الف انتخاب iاز10میشه به توان 2.
راه حل قسمت اول یه ایرادی داره . اونم اینه که توی اون فاکتوریله ، یه سریا ممکنه با خودشون متناظر بشن . بعد کلی حالت تکراری پیدا می کنه .
علاوه بر این فک کنم اونی که نوشتید ، باید حداکثر 9 تا باشه .
راه حلی که من برا این سوال دارم ، از یه مفهومی به عنوان پریش استفاده می کنه .
حالا پریش چیه ؟
با یه مثال توضیح می دم .
مثلا تو همین سوال ، اگه بیایم این 10 تا کلاهو ، طوری بین این نفر تقسیم کنیم ، که مطمئن باشیم به هیچ کس ، کلاه خودش نمی رسه ، ما یه پریش 10 تایی ساختیم .
فهمیدید پریش چیه ؟
پس ما اول باید یه راهی ارائه بدیم که تعداد پریش های n تایی رو اول محاسبه کنیم واسه این سوال .
یه راهی برای این محاسبه وجود داره ، که با استفاده از عدد e یا همون عدد نپر هستش . ( تو اینترنت ، هم می تونید در مورد e بیشتر مطالعه کنید ، هم شاید بتونید این فرمول رو بدست بیارید . )
اما یه راه استقرایی هم داره محاسبه این عدد . فرض کنید که ما ، تعداد پریش های 1 تا k تایی رو محاسبه کردیم . ( من راستش خودم علامتی که به عنوان "تعداد پریش های n تایی استفاده میشه رو بلد نیستم ! به اختصار می نویسم :"تپ(k)" ) حالا برای محاسبه تپ(k+1) ، از مکمل گیری استفاده می کنیم .
به این صورت که می گیم همه حالت های برداشتن این کلاه ها (یعنی (k+1)! ) منهای حالت هایی حداقل یه نفر کلا خودشو بر می داره .
مشابه روشی که آقای مهدی اون بالا گفتن ، میایم حالت بندی می کنیم رو تعداد کسایی که کلاه خودشونو بر می دارن . منتهی به جای اینکه اون انتخابه رو تو اون فاکتوریله ضرب کنیم ، تو تپ(k+1-i) ضرب می کنیم . پس ما الآن تپ (i+1) رو هم محاسبه کردیم به استقرا .
حالا پس جواب سوال ، میشه همونی که آقای مهدی نوشتن ، فقط به جای اون فاکتوریله ، باید تپ(10-i ) تو اون انتخاب ضرب شه .
البته این کل حالت هاست . پس احتمال کل ، میشه این عددی که بالا محاسبه کردیم ، تقسیم بر 10! .
یا در واقع ، جواب میشه 1 منهای حاصل تقسیم تپ(10) بر 10! .
اما برای قسمت دوم ، ایده من اینه که از قبلیه استفاده کنیم .
برای محاسبه کل حالت ها ، به نظر من به جای 10! حالت ، 10! × 10! حالت داریم . یعنی به 10! حالت ، میایم نوبت ها رو به آدما نسبت می دیم ، و به 10! حالت ، میایم آدما رو به کلاها نسبت می دیم .
برای محاسبه حالت های نامطلوب هم ، باید همه رو تو یه صف بچینیم ( یعنی به هر کسی نوبتی نسبت بدیم که 10! حالت داره ) و بعد یه پریش 10 تایی درست کنیم .
پس بازم جواب سوال ، می شه 1 منهای حاصل تقسیم 10! × تپ (10) بر !10×10! . یعنی احتمالش با بالایی یکیه !
برا اینکه یه کم شهود پیدا کنید ، که چرا این دو تا احتمال برابر شدن ، فک کنید که اگه مثلا تو حالت اول ، یه نفر با کلاهی که بهش نسبت می دیم رو حذف کنیم ، شرایطی که ایجاد میشه ، مثل حالتیه که وقتی تو قسمت دوم ، نفر اول کلاهشو برمیداره ، ایجاد میشه . در واقع ، ترتیب وایسادن اینا ، تو کلاهی که بهشون نسبت می دیم ، تاثیری نداره . چون هر کسیو و کلاهش ، مستقل از بقیه ن .
خیلی پیچیده شد

مهدی
کاربر فوقحرفهای

- ارسالها
- 1,112
- امتیاز
- 7,384
- نام مرکز سمپاد
- علامهحلی
- شهر
- تهران
- مدال المپیاد
- کامپیوتر
- دانشگاه
- دانشگاه تهران. :دی
- رشته دانشگاه
- آمار. :دی
پاسخ : سوالات ریاضی

خوب ،فک کنم کلا اشتباه کار کرده بودم و سوالو حتی اشتباه فهمیده بودم.
با تشکر از نیلوفر خانوم که یادم انداخت یه مبحثی هستی به نام پریشها
اصلا حواسم نبود به این مبحث
خوب برای حل سوال باید دو نکته اول بگم که دفعه قبل یادم رفت;
1-ترتیب اینکه چه کسی کلاه هارو برداره اصلا مهم نیست.
به فرض این افراد 3نفر باشند و شخص 1 کلاه 2 رو برداشته باشه ،شخص 2 کلاه 3 رو برداشته باشه.
شخص 3 هم کلاه 1 رو برداشته باشه.خوب این حالت باحالتی که ابتدا فرد 3کلاه1رو برمیداره
فرد1کلاه 2 رو برمیداره
و فرد 2کلاه 3 رو برمیداره هیچ فرقی نداره.
چون در آخر یکی هستن.
مثل مجموعه {1-2-3-4} که با مجموعه{2-4-3-1}هیچ فرقی نداره.
بنابراین قسمت 2 حذف میشه.
پ.ن باتشکر از فاطمه خانوم
2-نتیجه گرفتیم که قسمت 1و2 یکی هستند.
و راهی که میشه برای حل این مساله در پیش گرفت طبق گفته آقا سیاوش و نیلوفر خانوم پریش ها و اصل متمم هستند.
پریش رو که نیلوفر خانوم توضیح دادن و اصل متمم هم به این دلیله که برعکس حداقل 1میشه هیچی...
پس ما باید تعداد کل حالات رو که میشه10!رو از
پریش های این ده تا کم کنیم.
عدد به دست اومده میشه تعداد حالات مطلوب.
و جواب سوال میشه احتمال این که این حالات مطلوب دربیان از کل حالات که میشه
حالات مطلوب تقسیم بر کل حالات (10!)
و در ضمن پریش های یه مجموعه nتایی برابر است با. که در اینجا n=10


خوب ،فک کنم کلا اشتباه کار کرده بودم و سوالو حتی اشتباه فهمیده بودم.

با تشکر از نیلوفر خانوم که یادم انداخت یه مبحثی هستی به نام پریشها

اصلا حواسم نبود به این مبحث

خوب برای حل سوال باید دو نکته اول بگم که دفعه قبل یادم رفت;
1-ترتیب اینکه چه کسی کلاه هارو برداره اصلا مهم نیست.
به فرض این افراد 3نفر باشند و شخص 1 کلاه 2 رو برداشته باشه ،شخص 2 کلاه 3 رو برداشته باشه.
شخص 3 هم کلاه 1 رو برداشته باشه.خوب این حالت باحالتی که ابتدا فرد 3کلاه1رو برمیداره
فرد1کلاه 2 رو برمیداره
و فرد 2کلاه 3 رو برمیداره هیچ فرقی نداره.
چون در آخر یکی هستن.
مثل مجموعه {1-2-3-4} که با مجموعه{2-4-3-1}هیچ فرقی نداره.
بنابراین قسمت 2 حذف میشه.
پ.ن باتشکر از فاطمه خانوم
2-نتیجه گرفتیم که قسمت 1و2 یکی هستند.
و راهی که میشه برای حل این مساله در پیش گرفت طبق گفته آقا سیاوش و نیلوفر خانوم پریش ها و اصل متمم هستند.
پریش رو که نیلوفر خانوم توضیح دادن و اصل متمم هم به این دلیله که برعکس حداقل 1میشه هیچی...
پس ما باید تعداد کل حالات رو که میشه10!رو از
پریش های این ده تا کم کنیم.
عدد به دست اومده میشه تعداد حالات مطلوب.
و جواب سوال میشه احتمال این که این حالات مطلوب دربیان از کل حالات که میشه
حالات مطلوب تقسیم بر کل حالات (10!)
و در ضمن پریش های یه مجموعه nتایی برابر است با. که در اینجا n=10

- ارسالها
- 1,639
- امتیاز
- 28,325
- نام مرکز سمپاد
- ضروری
- شهر
- ضروری
- سال فارغ التحصیلی
- 0
پاسخ : سوالات ریاضی
دایره های A و B و C بر یکدیگر مماس خارجی اند و هر یک بر دایره ی D مماس داخل. دایره های B و C برابرند. شعاع دایره ی A برابر 1 است و از مرکز دایره ی D گذشته است. شعاع دایره ی B چقدر است؟
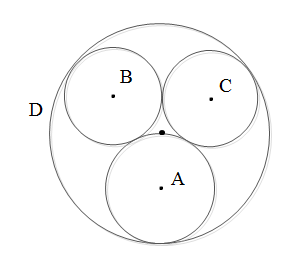
دایره های A و B و C بر یکدیگر مماس خارجی اند و هر یک بر دایره ی D مماس داخل. دایره های B و C برابرند. شعاع دایره ی A برابر 1 است و از مرکز دایره ی D گذشته است. شعاع دایره ی B چقدر است؟





